
【题目】二次函数![]() (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是
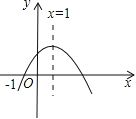
A. a>0 B. 当﹣1<x<3时,y>0
C. c<0 D. 当x≥1时,y随x的增大而增大
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.
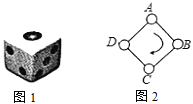
(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
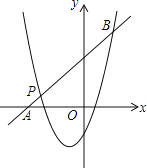
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:其中说法正确的是( )①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
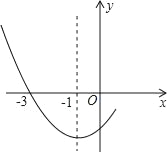
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,﹣2),B(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,且点D纵坐标为t,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于点A(![]() ,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
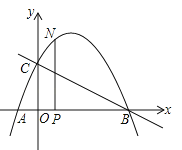
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(![]() ),求△ABN的面积S与t的函数关系式;
),求△ABN的面积S与t的函数关系式;
(3)若![]() 且
且![]() 时△OPN∽△COB,求点N的坐标.
时△OPN∽△COB,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )

A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com