【题目】在平面直角坐标系xOy中，抛物线y=2x2+mx+n经过点A（0，﹣2），B（3，4）.
(1)求抛物线的表达式及对称轴；
(2)设点B关于原点的对称点为C，点D是抛物线对称轴上一动点，且点D纵坐标为t，记抛物线在A，B之间的部分为图象G（包含A，B两点）.若直线CD与图象G有公共点，结合函数图象，求点D纵坐标t的取值范围.
【答案】（1）y=2x2﹣4x﹣2，对称轴为直线x=1；（2）﹣4≤t≤
．见解析。
【解析】
（1）将A与B坐标代入抛物线解析式求出m与n的值，确定出抛物线解析式，求出对称轴即可；
（2）由题意确定出C坐标，以及二次函数的最小值，确定出D纵坐标的最小值，求出直线BC解析式，令x=1求出y的值，即可确定出t的范围．
（1）∵抛物线y=2x2+mx+n经过点A（0，﹣2），B（3，4），代入得：
，解得：
，∴抛物线解析式为y=2x2﹣4x﹣2，y=2x2﹣4x﹣2=
，∴对称轴为直线x=1；
（2）由题意得：C（﹣3，﹣4），二次函数y=2x2﹣4x﹣2=的最小值为﹣4，由函数图象得出D纵坐标最小值为﹣4，设直线BC解析式为y=kx+b，将B与C坐标代入得：
，解得：k
，b=0，∴直线BC解析式为yx，当x=1时，y，则t的范围为﹣4≤t
．
科目：初中数学 来源： 题型：
【题目】如图，己知AB是⊙O的直径，AC是弦，点P是BA延长线上一点，连接PC，BC．∠PCA=∠B．
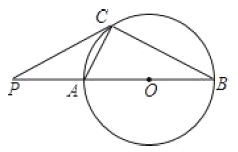
（1）求证：PC是⊙O的切线；
（2）若PC=6，PA=4，求直径AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC是
的直径，AB与相切于点A，四边形ABCD是平行四边形，BC交于点E．
判断直线CD与的位置关系，并说明理由；
若的半径为5cm，弦CE的长为8cm，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
（a≠0）的图象如图所示，则下列结论中正确的是
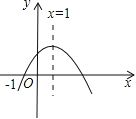
A. a＞0 B. 当﹣1＜x＜3时，y＞0
C. c＜0 D. 当x≥1时，y随x的增大而增大
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c的图象如图所示．下列结论：①abc＞0；②2a﹣b＜0；③4a﹣2b+c＜0；④（a+c）2＜b2其中正确的个数有（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】炮弹的运行轨道若不计空气阻力是一条抛物线．现测得我军炮位A与射击目标B的水平距离为600m，炮弹运行的最大高度为1200m.
(1)求此抛物线的解析式；
(2)若在A、B之间距离A点500m处有一高350m的障碍物，计算炮弹能否越过障碍物.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实根，且其中一个根为另一根的2倍，则称这样的方程为“倍根方”，以下关于倍根方程的说法正确的是______（填正确序号）
①方程x2﹣x﹣2=0是倍根方程．
②若（x﹣2）（mx+n）=0是倍根方程，则4m2+5mn+n2=0．
③若点（p，q）在反比例函数y=
的图象上，则关于x的方程px2+3x+q=0是倍根方程．
④若方程ax2+bx+c=0是倍根方程且相异两点M（1+t，s）、N（4﹣t，s）都在抛物线y=ax2+bx+c上，则方程ax2+bx+c=0必有一个根为
．
查看答案和解析>>
科目：初中数学 来源： 题型：
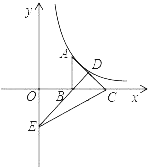
【题目】如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC上的中线BD反向延长线交y轴负半轴于E，双曲线y＝
(x>0)的图象经过点A，若S△BEC＝8，则k＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点O (0，0)，A (－5，0)，B (2，1)，抛物线
(h为常数)与y轴的交点为C。
(1) 抛物线经过点B，求它的解析式，并写出此时抛物线的对称轴及顶点坐标；
(2)设点C的纵坐标为
，求的最大值，此时抛物线上有两点
，
，其中
，比较
与
的大小；
(3)当线段OA被只分为两部分，且这两部分的比是1：4时，求h的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com