
【题目】在平面直角坐标系xOy中,抛物线![]() 的对称轴与x轴交于点A.
的对称轴与x轴交于点A.
(1)A的坐标为 (用含a的代数式表示);
(2)若抛物线与x轴交于P,Q两点,且PQ=2,求抛物线的解析式.
(3)点B的坐标为![]() ,若该抛物线与线段AB恰有一个公共点,结合函数图象,直接写出a的取值范围.
,若该抛物线与线段AB恰有一个公共点,结合函数图象,直接写出a的取值范围.
科目:初中数学 来源: 题型:
【题目】在图的方格纸中,△OAB的顶点坐标分别为O(0,0)、A(-2,-1)、B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.

(1)在图中标出位似中心P的位置,并写出点P的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1.并写出点B的对应点B2的坐标;
(3)判断△OA2B2能否看作是由△O1A1B1经过某种变换后得到的图形,若是,请指出是怎样变换得到的(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
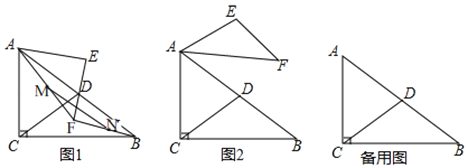
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD为AB边上的中线.在Rt△AEF中,∠AEF=90°,AE=EF,AF<AC.连接BF,M,N分别为线段AF,BF的中点,连接MN.
(1)如图1,点F在△ABC内,求证:CD=MN;
(2)如图2,点F在△ABC外,依题意补全图2,连接CN,EN,判断CN与EN的数量关系与位置关系,并加以证明;
(3)将图1中的△AEF绕点A旋转,若AC=a,AF=b(b<a),直接写出EN的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是半圆O上的一点,AB是⊙O的直径,D是![]() 的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
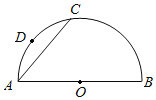
下面是小明的做法,请帮他补充完整(包括补全图形)
解:补全半圆O为完整的⊙O,连接AD,延长DE交⊙O于点H(补全图形)
∵D是![]() 的中点,
的中点,
∴![]() .
.
∵DE⊥AB,AB是⊙O的直径,
∴![]() ( )(填推理依据)
( )(填推理依据)
∴![]()
∴∠ADF=∠FAD( )(填推理依据)
∴AF=DF( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
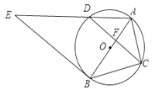
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com