
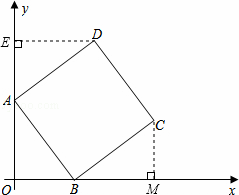
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
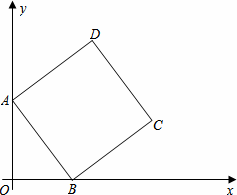
【解析】(1)x2﹣7x+12=0,解得x1=3,x2=4,∵OA>OB,∴OA=4,OB=3,过D作DE⊥y于点E,∵正方形ABCD,∴AD=AB,∠DAB=90°,∠DAE+∠OAB=90°,∠ABO+∠OAB=90°,∴∠ABO=∠DAE,∵DE⊥AE,∴∠AED=90°=∠AOB,∵DE⊥AE∴∠AED=90°=∠AOB,
∴△DAE≌△ABO(AAS),∴DE=OA=4,AE=O B=3,∴OE=7,∴D(4,7);
B=3,∴OE=7,∴D(4,7);
(2)过点C作CM⊥x 轴于点M,
轴于点M,
同上可证得△BCM≌△ABO,∴CM=OB=3,BM=OA=4,∴OM=7,∴C(7,3),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),代入B(3,0),C(7,3)得, ,
,
解得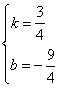 ,∴y=
,∴y=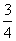 x﹣
x﹣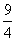 ;
;
(3)存在.
点P与点B重合时,P1(3,0),
点P与点B关于点C对称时,P2(11,6).


科目:初中数学 来源: 题型:
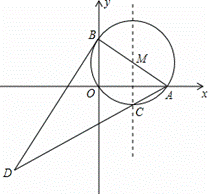
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是 ( )

(A)正三角形 (B)正方形 (C)正五边形 (D)正六边形
查看答案和解析>>
科目:初中数学 来源: 题型:
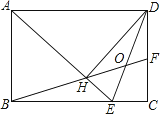
如图,在矩形ABCD中,AD=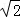 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求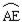 的长.
的长.
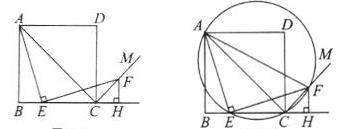
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com