
如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求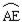 的长.
的长.
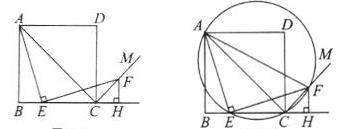
图1 图2
(1)BE=FH ;理由见解析
(2)证明见解析
(3)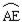 =2π
=2π
【解析】(1)BE=FH。理由如下:
∵四边形ABCD是正方形 ∴∠B=90°,∵FH⊥BC , ∴∠FHE=90°,又∵∠AEF=90°,∴∠AEB+∠HEF=90°, 且∠BAE+∠AEB=90°,∴∠HEF=∠BAE ,∴ ∠AEB=∠EFH ,又∵AE=EF,∴△ABE≌△EHF(SAS),∴BE=FH;
(2)∵△ABE≌△EHF,∴BC=EH,BE=FH , 又∵BE+EC=EC+CH,∴BE=CH,∴CH=FH,∴∠FCH=45°,∴∠FCM=45°,∵AC是正方形对角线,∴ ∠ACD=45°,∴∠ACF=∠FCM +∠ACD =90°;
(3)∵AE=EF,∴△AEF是等腰直角三角形,△AEF外接圆的圆心在斜边AF的中点上。设该中点为O。连结EO得∠AOE=90°
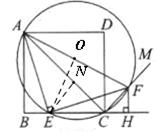
过E作EN⊥AC于点N,Rt△ENC中,EC=4,∠ECA=45°,∴EN=NC=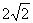 ,Rt△ENA中,EN =
,Rt△ENA中,EN =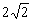 ,又∵∠EAF=45°,∠CAF=∠CEF=15°(等弧对等角),∴∠EAC=30°,∴AE=
,又∵∠EAF=45°,∠CAF=∠CEF=15°(等弧对等角),∴∠EAC=30°,∴AE=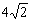 ,Rt△AFE中,AE=
,Rt△AFE中,AE=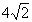 = EF,∴AF=8, AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°,
= EF,∴AF=8, AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°, =2π·4·(90°÷360°)=2π.
=2π·4·(90°÷360°)=2π.


科目:初中数学 来源: 题型:
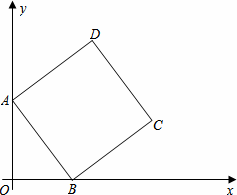
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
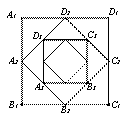
小宋作出了边长为2的第一个正方形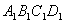 ,算出了它的面积.然后分别取正方形
,算出了它的面积.然后分别取正方形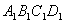 四边的中点
四边的中点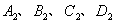 作出了第二个正方形
作出了第二个正方形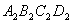 ,算出了它的面积.用同样的方法,作出了
,算出了它的面积.用同样的方法,作出了
第三个正方形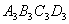 ,算出了它的面积 ,由此可得,第六个正方形
,算出了它的面积 ,由此可得,第六个正方形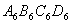 的面积
的面积
是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数的图象与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3)
(1)求二次函数的解析式
(2)在抛物线的对称轴上确定一点P,使得△ACQ的周长最小,并求出点P的坐标和△ACQ的周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com