2-2：在三角形ABC中，若AB=4，BC=5，AC=4，则三角形ABC是 三角形。
科目：初中数学 来源： 题型：
如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC.
(1) 试判断BE与FH的数量关系，并说明理由；
(2) 求证：∠ACF=90°；
(3) 连接AF，过A，E，F三点作圆，如图2. 若EC=4，∠CEF=15°，求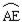
的长.
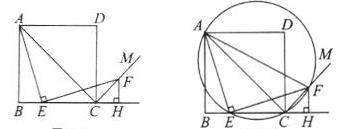
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
某五金店购进一批数量足够多的p型节能电灯 进价为35元／只，以50元／只销售，每天销售20只．市场调研发现：若每只每降l元，则每天销售数量比原来多3只．现商店决定对Q型节能电灯进行降价促销活动，每只降价x元（x为正整数）．在促销期间，商店要想每天获得最大销售利润，每只应降价多少元?每天最大销售毛利润为多少?（注：每只节能灯的销售毛利润指每只节能灯的销售价与进货价的差）
查看答案和解析>>
科目：初中数学 来源： 题型：
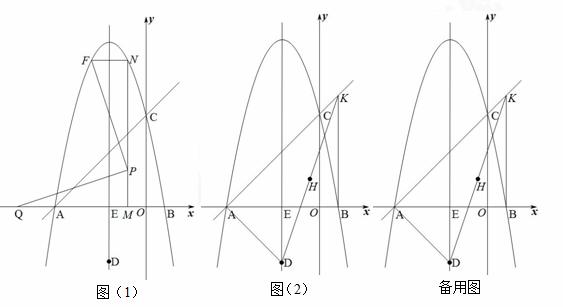
如图（1），抛物线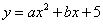
（
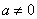）与x轴交于A、B两点，与y轴交于点C，直线AC的解析式为
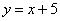，抛物线的对称轴与
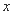轴交于点E，点D（－2，－3）在对称轴上．
（1）求此抛物线的解析式；
（2）如图（1），若点M是线段OE上一点（点M不与点O、E重合），过点M作MN⊥x轴，交抛物线于点N，记点N关于抛物线对称轴的对称点为点F，点P是线段MN上一点，且满足MN=4MP，连接FN、FP，作QP⊥PF交x轴于点Q，且满足PF=PQ，求点Q的坐标；
（3）如图（2），过点B作BK⊥x轴交直线AC于点K，连接DK、AD，点H是DK的中点，点G是线段AK上任意一点，将△DGH沿GH边翻折得△DGH，求当KG为何值时，△DGH与△KGH重叠部分的面积是△DGK面积的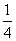
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
格点上，则与△ABC相似的三角形所在的网格图形是图 （ ）．
