
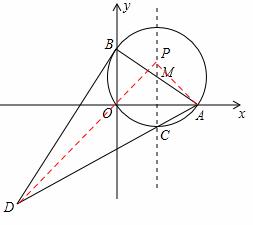
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
(1) ;(2)证明见解析;(3)取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值,为
;(2)证明见解析;(3)取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值,为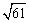 .
.
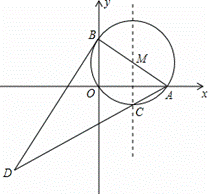
【解析】(1)∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,∴AB=5.∴圆的半径为 .
.
(2)由题意可得出:M(2,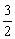 ).∵C为劣弧AO的中点,由垂径定理且 MC=
).∵C为劣弧AO的中点,由垂径定理且 MC= ,故 C(2,﹣1).如答图1,过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 N,则△ACN∽△ADH,又∵DC=4AC,∴ DH=5NC=5,HA=5NA=10.∴D(﹣6,﹣5).
,故 C(2,﹣1).如答图1,过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 N,则△ACN∽△ADH,又∵DC=4AC,∴ DH=5NC=5,HA=5NA=10.∴D(﹣6,﹣5).
设直线BD表达式为:y=ax+b,则 ,解得:
,解得: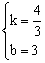 .∴直线BD表达式为:y=
.∴直线BD表达式为:y= x+3.
x+3.
设 BD 与 x 轴交于Q,则Q(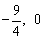 ).∴OQ=
).∴OQ= .∴
.∴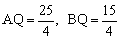 .
.
∵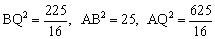 ,∴
,∴ .∴△ABQ是直角三角形,即∠ABQ=90°.
.∴△ABQ是直角三角形,即∠ABQ=90°.
∴BD⊥AB,BD为⊙M的切线.
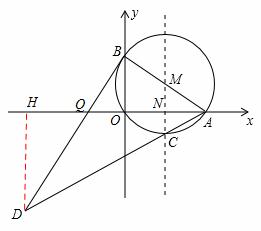
(3)如答图2,取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值.
设直线DO表达式为 y=kx,∴﹣5=﹣6k,解得:k=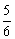 .∴直线DO表达式为 y=
.∴直线DO表达式为 y=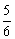 x
x
又∵在直线DO上的点P的横坐标为2,∴y=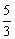 .∴P(2,
.∴P(2,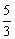 ).此时|DP﹣AP|=DO=
).此时|DP﹣AP|=DO=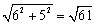 .
.


科目:初中数学 来源: 题型:
周末,身高都为1.6 m的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在 处测得她看塔顶的仰角
处测得她看塔顶的仰角 为
为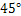 ,小丽站在
,小丽站在 处测得她看塔顶的仰角
处测得她看塔顶的仰角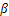 为30°.她们又测出
为30°.她们又测出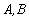 两点的距离为30 m.假设她们的眼睛离头顶
两点的距离为30 m.假设她们的眼睛离头顶 都为
都为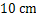 ,则可计算出塔高约为(结果精确到
,则可计算出塔高约为(结果精确到 ,参考数据:
,参考数据: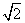
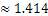 ,
,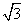
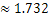 )( )
)( )
A.36.21 m B.37.71 m C.40.98 m D.42.48 m
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
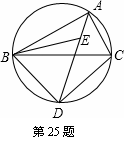
如图:△ 内接于⊙
内接于⊙ ,∠
,∠ 与∠
与∠ 的角平分线
的角平分线 相交于点
相交于点 ,延长
,延长 交⊙
交⊙ 于点
于点 ,连接
,连接 ,
, ,且∠
,且∠

(1)求∠ 的大小;
的大小;
(2)求证:△ 为等边三角形;
为等边三角形;
(3)若∠ ,⊙
,⊙ 的半径为
的半径为 ,求等边三角形
,求等边三角形 的边长.
的边长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
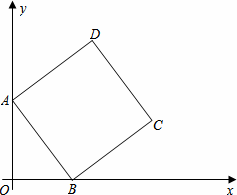
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
我国经济飞速发展,2014年的GDP为63.6万亿元,用科学记数法表示63.6万亿元为( )
A.0.636×106亿元 B.6.36×105亿元
C.6.36×104亿元 D.63.6×105亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com