
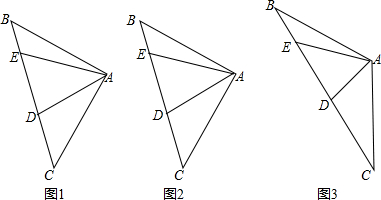
分析 (1)作DG⊥AC于G,证明出△ABC是等腰直角三角形,进而求出AG的长,即可求出BC的长;
(2)作DH⊥AE于H,设DC=a,利用a表示出BC、DE和CD的长,根据线段之间的关系得到结论;
(3)作DG⊥AC于G,AH⊥BC于H,设DC=2a,还是利用a表示出BC、DE和CD的长,即可表示出线段DC和BE之间的数量关系.
解答 解:(1)如图1所示,作DG⊥AC于G,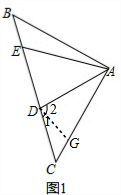
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠1=∠B=45°,
∵∠ADE=75°,
∴∠2=60°,∠DAG=30°,
∴DG=CG=$\frac{\sqrt{2}}{2}$CD=1,AD=2DG=2,
∴AG=$\sqrt{A{D}^{2}-D{G}^{2}}$=$\sqrt{3}$,
∴AC=AG+CG=$\sqrt{3}$+1,
∴BC=$\sqrt{2}$AG=$\sqrt{6}$+$\sqrt{2}$;
(2)如图2所示,作DH⊥AE于H,设DC=a,则DG=CG=$\frac{\sqrt{2}}{2}$a,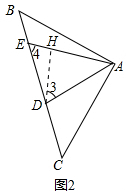
∴AD=2DG=$\sqrt{2}$a,AG=$\frac{\sqrt{6}}{2}$a,
∴AC=AG+CG=$\frac{\sqrt{6}+\sqrt{2}}{2}$a,
∴BC=$\sqrt{2}$AC=($\sqrt{3}$+1)a,
∵∠EAD=45°,
∴△ADH是等腰直角三角形,
∴AH=DH=$\frac{\sqrt{2}}{2}$AD=a,
∵∠4=180°-∠ADE-∠DAE=60°,
∴DE=2EH,
∴DE=DH÷$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$a,
∴BE=BC-DE-CD=$\frac{\sqrt{3}}{3}$a=$\frac{\sqrt{3}}{3}$DC,
∴DC=$\sqrt{3}$BE;
(3)(2)中的结论不成立,理由如下: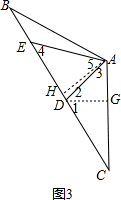
如图3所示,作DG⊥AC于G,AH⊥BC于H,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∴∠1=60°,
又∵∠ADE=75°,∠DAE=60°,
∴∠2=∠3=∠4=∠5=45°,
设DC=2a,则DG=AG=a,CG=$\sqrt{3}$a,
∴AC=AG+CG=($\sqrt{3}$+1)a,
∴EH=AH=$\frac{1}{2}$AC=$\frac{\sqrt{3}+1}{2}$a,CH=$\frac{\sqrt{3}}{2}$AC=$\frac{3+\sqrt{3}}{2}$a,
∴BC=2CH=(3+$\sqrt{3}$)a,DH=CH-DC=$\frac{\sqrt{3}-1}{2}$a,
∴DE=EH+DH=$\sqrt{3}$a,
∴BE=BC-DE-DC=(3+$\sqrt{3}$)a-$\sqrt{3}$a-2a=a=$\frac{1}{2}$DC,
∴DC=2BE.
点评 本题主要考查相似形综合题,此题涉及到勾股定理、等腰三角形的判定与性质等知识,解答本题的关键是正确作出辅助线,构造特殊的直角三角形,利用直角三角形的性质以及勾股定理解决线段的长度,此题有一定的难度.


科目:初中数学 来源: 题型:选择题
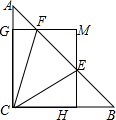 如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=
如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
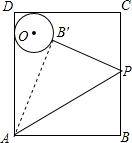 如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.
如图,矩形ABCD中,AB=20,AD=25,矩形内有一点O,以O为圆心,5为半径画圆,与AD,CD都相切,点P是BC上一点,将△ABP沿着AP对折得到△AB′P,若AB′与⊙O相切于点B′.则BP的长度是12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
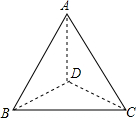 如图是正四面体(四个面都是正三角形的三棱锥)小木块(质地均匀)的一个顶点,将木块随机投掷在水平桌面上.则A与桌面接触的概率是$\frac{3}{4}$.
如图是正四面体(四个面都是正三角形的三棱锥)小木块(质地均匀)的一个顶点,将木块随机投掷在水平桌面上.则A与桌面接触的概率是$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 900° | B. | 1260° | C. | 1440° | D. | 1800° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com