

分析 通过观察图形的变化可得:每增加一条鱼就会增加6根火柴,按照这个规律搭下去,火柴的总数是一个等差数列的和.先根据规律求出第五个图形中的火柴棒是2+6×5=32根,再求出一般规律2+6n,最后把火柴总数137-3=134代入一般规律求出n的值即为“鱼”的数目.
解答 解:观察图形可知
第一个图共有火柴棒2+6=2+6×1=8根,有1条鱼;
第二个图共有火柴棒2+6+6=2+6×2=14根,有2条鱼;
第三个图共有火柴棒2+6+6+6=2+6×3=20根,有3条鱼;
第四个图共有火柴棒2+6+6+6+6=2+6×4=26根,有4条鱼;
第五个图共有火柴棒2+6+6+6+6+6=2+6×5=32根,有5条鱼;
…
第n个图共有火柴棒(2+6n)根,有n条鱼;
设n条鱼共用了火柴棒137-3=134根,即2+6n=134,解得n=22
所以小明搭了22条“小鱼”
故答案为:(1)2+6n;(2)32;(3)小明搭了22条“小鱼”.
点评 本题主要考查了如何从变化的图形中找规律,并用规律解题.注意本题中主要是根据火柴的总数是一个等差数列的和来得到一般规律.要把变化的数据分成不变的量和变化的量两个部分,把变化的部分与图形的序号找出对应关系是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
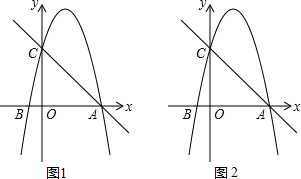
 在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明想测量院子里一棵树的高度,在某一时刻,他站在该树的影子上,前后移动,直到他本身的影子的顶端正好与树影的顶端重叠.此时,他与该树的水平距离2m,小明身高1.5m,他的影长是1.2m,那么该树的高度为4m.
如图,小明想测量院子里一棵树的高度,在某一时刻,他站在该树的影子上,前后移动,直到他本身的影子的顶端正好与树影的顶端重叠.此时,他与该树的水平距离2m,小明身高1.5m,他的影长是1.2m,那么该树的高度为4m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com