
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
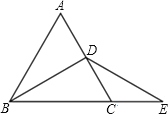
(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
【答案】(1)证明见解析(2)48
【解析】试题分析:(1)根据等边三角形的性质得到∠ABC=∠ACB=60°,∠DBC=30°,再根据角之间的关系求得∠DBC=∠CED,根据等角对等边即可得到DB=DE;(2)根据直角三角形中,30°的锐角所对的直角边等于斜边的一半DC=8,AC=16,即可求得△ABC的周长.
试题解析:
(1)证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
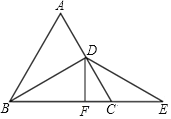
(2)解: ∵∠CDE=∠CED=![]() ∠BCD=30°,
∠BCD=30°,
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.


科目:初中数学 来源: 题型:
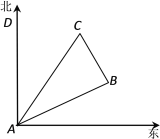
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,12),点C的坐标为(-4,0),且tan∠ACO=2.
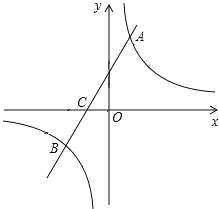
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=![]() a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=
a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=![]() A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
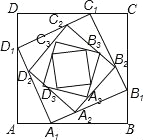
A.![]() B.(
B.(![]() )na2 C.(
)na2 C.(![]() )n-1a2 D.(
)n-1a2 D.(![]() )na2
)na2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB = 6cm,AD=10 cm,点P在AD 边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
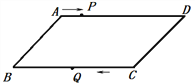
A. 1 次 B. 2次 C. 3次 D. 4次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在BC上,且CE=![]() BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=
BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=![]() S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
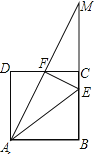
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com