
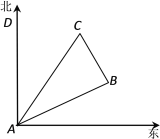
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
【答案】(1)10km;(2)点C在点A的北偏东30°的方向上
【解析】试题分析: (1)根据所走的方向可判断出△ABC是直角三角形,根据勾股定理可求出解.
(2)求出∠DAC的度数,即可求出方向.
试题解析:
(1)过B点作直线EF∥AD,
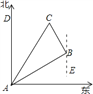
∴∠DAB=∠ABF=60°,
∵∠EBC=30°,
∴∠ABC =180°―∠ABF―∠EBC= 180°―60°―30°=90°,
∴ △ABC为直角三角形,由已知可得:BC=5km,AB=![]() km,
km,
由勾股定理可得:AC2=BC2+AB2,
所以AC=![]() =10(km),
=10(km),
即:A、C两点之间的距离为10km
(2)在Rt△ABC中, ∵BC=5km,AC=10km,∴∠CAB=30°,
∵∠DAB=60°,∴∠DAC=30°,
即点C在点A的北偏东30°的方向上.
点睛;勾股定理本身就是数形结合的一个典范,它把直角三角形有一个直角的“形”的特点,转化为三边“数”的关系,利用勾股定理解决实际问题,关键是利用数形结合思想将实际问题转化为直角三角形模型,再利用方程来解决.


科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a<b,则 3a________ 3b, -a+1________-b+1,
(m2+1)a_______(m2+1)b.(用“ >”,“ <”或“=”填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果在同一平面内有两个图形甲和乙,通过平移,总可以完全重合在一起(不论甲和乙的初始位置如何),则甲和乙是( ).
A. 两个点 B. 两个半径相等的圆
C. 两个点或两个半径相等的圆 D. 两个能够完全重合的多边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
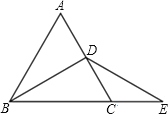
(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com