
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
【答案】
(1)解:连接OE,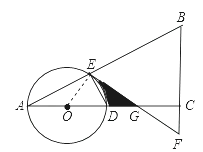
∵OA=OE,∴∠A=∠AEO,
∵BF=EF,∴∠B=∠BEF,
∵∠ACB=90°,∴∠A+∠B=90°,∴∠AEO+∠BEF=90°,
∴∠OEG=90°,∴EF是⊙O的切线;
(2)解:∵AD是⊙O的直径,∴∠AED=90°,
∵∠A=30°,∴∠EOD=60°,∴∠EGO=30°,
∵AO=2,∴OE=2,∴EG=2 ![]() ,
,
∴阴影部分的面积= ![]() =
= ![]() .
.
【解析】(1)要证直线EF与⊙O的位置关系,连接OE,只需证明OE⊥EF。根据等腰三角形的性质证出∠A=∠AEO,∠B=∠BEF,根据∠ACB=90°得出∠A+∠B=90°,可证得∠AEO+∠BEF=90°,根据切线的判定即可证得结论。
(2)根据圆周角定理可证得∠AED=90°,∠EOD=60°,再利用解直角三角形求出EG的长,然后根据阴影部分的面积=△OEG的面积-扇形EOD的面积,计算即可得出答案。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC边长为10,P在AB上,Q在BC延长线,CQ=PA,过点P作PE⊥AC点E,过点P作PF∥BQ,交AC边于点F,连接PQ交AC于点D,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为![]() ),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点
),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点![]()
![]()
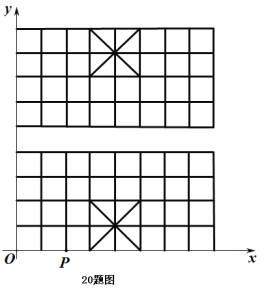
![]() 写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);
写出下一步“马”可能到达的点的坐标为_ (写出所有可能的点的坐标);
![]() 顺次连接
顺次连接![]() 中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;
中的所有点,得到的图形是 _图形(填“中心对称”或“轴对称”;
![]() 将
将![]() 中得到的图形各顶点的坐标都乘以
中得到的图形各顶点的坐标都乘以![]() 请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是微信朋友圈热传的一篇文章.国际上,法国教育部宣布从2018年9月新学期起,小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数是![]() 人.
人.

请你根据以上信息解答下列问题:
![]() 求出本次随机抽取的学生共有多少人;
求出本次随机抽取的学生共有多少人;
![]() 在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
![]() 补全条形统计图;
补全条形统计图;
![]() 该校共有学生
该校共有学生![]() 人,估计每周使用手机时间在
人,估计每周使用手机时间在![]() 小时以上(不含
小时以上(不含![]() 小时)的人数.
小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.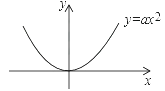
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知,![]() 满足
满足![]() 点在
点在![]() 轴的负半轴上,直角顶点
轴的负半轴上,直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上方.
轴上方.
![]() 如图1所示,若点
如图1所示,若点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标是 ;
的坐标是 ;

![]() 如图2所示,若点
如图2所示,若点![]() 的坐标是
的坐标是![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,请求出点
,请求出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com