
【题目】如图,在△ABC中,AB=AC,BC=12,sinC=![]() ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.

【答案】cos∠CBD=![]()
【解析】试题分析:
如下图,连接AG并延长交BC于点H,由已知条件易得BH=CH=6,AG=2GH,AH⊥BC于点H,由sinC=![]() 设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=
设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=![]() ,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
试题解析:
如图连接AG延长AG交BC于H.
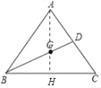
∵G是重心,
∴BH=CH=6,AG=2GH,
∵AB=AC,
∴AH⊥BC,
∵sin∠C=![]() ,设AH=4k,AC=5k,
,设AH=4k,AC=5k,
在Rt△AHC中,∵AH2+CH2=AC2,
∴(4k)2+62=(5k)2,
解得k=2,
∴AH=8,AC=10,
∴GH=![]() ,
,
在Rt△BGH中,BG=![]() ,
,
∴cos∠CBD=![]() .
.


科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的的偶数相加,它们的和的情况如下表:

(1)根据上面的等式,你能发现当n个连续的的偶数相加时,它们的和S=2+4+6+8+……+2n= .
(2)并按照此规律计算:①2+4+6+……300的值;②162+164+166+……+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若同时购进A种跳绳10根和B种跳绳7根,则共需395元,若同时购进A种跳绳5根和B种跳绳3根,共需185元
(1)求A、B两种跳绳的单价各是多少?
(2)若该商店准备同时购进这两种跳绳共100根,且A种跳绳的数量不少于跳绳总数量的![]() .若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
.若每根A种跳绳的售价为26元,每根B种跳绳的售价为30元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为______,中位数为_______;
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
(1)稿费不高于800元的不纳税;
(2)稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
(3)稿费为4000元或高于4000元的应缴纳全部稿费的11%的税,
试根据上述纳税的计算方法作答:
①若王老师获得的稿费为2400元,则应纳税________元,若王老师获得的稿费为4000元,则应纳税________元.
②若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
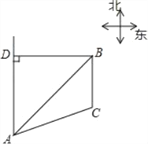
【题目】已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)(参考数据:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com