
【题目】如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠C,且点D、F分别在边AB、AC上.
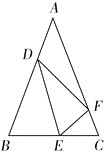
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:DE平分∠BDF.
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)根据等腰三角形的性质得到∠B=∠C,根据三角形的内角和和平角的定义得到∠BDE=∠CEF,于是得到结论;
(2)由(1)可得![]() ,根据点E是BC的中点,则可化为
,根据点E是BC的中点,则可化为![]() ,即可证:△DEF∽△ECF,则有△BDE∽△EDF,∠BDE=∠EDF,可得DE平分∠BDF.
,即可证:△DEF∽△ECF,则有△BDE∽△EDF,∠BDE=∠EDF,可得DE平分∠BDF.
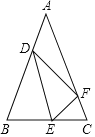
解:(1)∵AB=AC,
∴∠B=∠C=∠DEF,
∵∠BDE=180°-∠B-∠DEB,
∠CEF=180°-∠DEF-∠DEB,
∴∠BDE=∠CEF,
∴△BDE∽△CEF;
(2)∵△BDE∽△CEF,
∴![]() ,
,
∵点E是BC的中点,
∴BE=CE,
∴![]()
∵∠DEF=∠B=∠C,
∴△DEF∽△ECF,
∴△BDE∽△EDF,
∴∠BDE=∠EDF,
∴DE平分∠BDF.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-1)x+k2 =0有两个实数根x1.x2.
(1)求实 数k的取值范围;
(2)若(x1+1)(x2+1)=2,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)证明:DF是⊙O的切线;
(2)若AC=3AE,FC=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
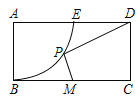
【题目】如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在弧BE上运动,则PM+![]() DP的最小值为____________.
DP的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件。
(1)当销售价格上涨时,请写出每天的销售量![]() (件)与销售价格
(件)与销售价格![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(2)如果要求每天的销售量不少于10件,且每件文具的利润至少为25元,问当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规作出这个输水管道的圆形截面的圆心(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8 cm,水面最深地方的高度为2 cm,求这个圆形截面的半径.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数![]() 的图象与性质,下列结论错误的是( )
的图象与性质,下列结论错误的是( )
A.当x=-2时,函数有最大值-3
B.当x<-2时,y随x的增大而增大
C.抛物线可由![]() 经过平移得到
经过平移得到
D.该函数的图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,求两盏景观灯之间的水平距离(提示:请建立平面直角坐标系后,再作答).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com