
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬AЈ¬BОӘxЦбЙПБҪөгЈ¬CЎўDОӘyЦбЙПөДБҪөгЈ¬ҫӯ№эөгAЈ¬CЈ¬BөДЕЧОпПЯөДТ»Іҝ·ЦC2ЧйәПіЙТ»Мх·вұХЗъПЯЈ¬ОТГЗ°СХвМх·вұХЗъПЯіЙОӘЎ°ө°ПЯЎұЈ®ТСЦӘөгCөДЧшұкОӘЈЁ0Ј¬©Ғ ![]() Ј©Ј¬өгMКЗЕЧОпПЯC2Јәy=mx2©Ғ2mx©Ғ3mЈЁmЈј0Ј©өД¶ҘөгЈ®
Ј©Ј¬өгMКЗЕЧОпПЯC2Јәy=mx2©Ғ2mx©Ғ3mЈЁmЈј0Ј©өД¶ҘөгЈ®
ЈЁ1Ј©ЗуAЎўBБҪөгөДЧшұкЈ»
ЈЁ2Ј©Ў°ө°ПЯЎұФЪөЪЛДПуПЮЙПКЗ·сҙжФЪТ»өгPЈ¬К№өГЎчPBCөДГж»эЧоҙуЈҝИфҙжФЪЈ¬ЗуіцЎчPBCГж»эөДЧоҙуЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©
ҪвЈәЎЯy=mx2©Ғ2mx©Ғ3m=mЈЁx©Ғ3Ј©ЈЁx+1Ј©Ј¬ЗТmЎЩ0Ј¬
Ўаөұy=0КұЈ¬ҝЙөГmЈЁx©Ғ3Ј©ЈЁx+1Ј©=0Ј¬ҪвөГx1=©Ғ1Ј¬x2=3Ј¬
ЎаAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁ3Ј¬0Ј©Ј»
ЈЁ2Ј©
ҪвЈәЙи№эAЎўBЎўCИэөгөДЕЧОпПЯҪвОцКҪОӘy=ax2+bx+cЈ¬
ФтУР  Ј¬ҪвөГ
Ј¬ҪвөГ  Ј¬
Ј¬
ЎаЕЧОпПЯC1ҪвОцКҪОӘy= ![]() x2©Ғx©Ғ
x2©Ғx©Ғ ![]() Ј¬
Ј¬
ИзНјЈ¬№эөгPЧчPQЎОyЦбЈ¬Ҫ»BCУЪQЈ¬
ЙиЦұПЯBCҪвОцКҪОӘy=kx+sЈ¬ФтУР  Ј¬ҪвөГ
Ј¬ҪвөГ  Ј¬
Ј¬
ЎаЦұПЯBCөДҪвОцКҪОӘy= ![]() x©Ғ
x©Ғ ![]() Ј¬
Ј¬
ЙиPЈЁxЈ¬ ![]() x2©Ғx©Ғ
x2©Ғx©Ғ ![]() Ј©Ј¬ФтQЈЁxЈ¬
Ј©Ј¬ФтQЈЁxЈ¬ ![]() x©Ғ
x©Ғ ![]() Ј©Ј¬
Ј©Ј¬
ЎаPQ= ![]() x©Ғ
x©Ғ ![]() ©ҒЈЁ
©ҒЈЁ ![]() x2©Ғx©Ғ
x2©Ғx©Ғ ![]() Ј©=©Ғ
Ј©=©Ғ ![]() x2+
x2+ ![]() xЈ¬
xЈ¬
ЎаSЎчPBC= ![]() PQOB=
PQOB= ![]() ЎБЈЁ©Ғ
ЎБЈЁ©Ғ ![]() x2+
x2+ ![]() xЈ©ЎБ3=©Ғ
xЈ©ЎБ3=©Ғ ![]() ЈЁx©Ғ
ЈЁx©Ғ ![]() Ј©2+
Ј©2+ ![]() Ј¬
Ј¬
ЎЯ©Ғ ![]() Јј0Ј¬
Јј0Ј¬
Ўаөұx= ![]() КұЈ¬SЎчPBCУРЧоҙуЦөЈ¬SЧоҙу=
КұЈ¬SЎчPBCУРЧоҙуЦөЈ¬SЧоҙу= ![]() Ј¬
Ј¬
![]() ЎБЈЁ
ЎБЈЁ ![]() Ј©2©Ғ
Ј©2©Ғ ![]() ©Ғ
©Ғ ![]() =©Ғ
=©Ғ ![]() Ј¬ҙЛКұPөгЧшұкОӘЈЁ
Ј¬ҙЛКұPөгЧшұкОӘЈЁ ![]() Ј¬©Ғ
Ј¬©Ғ ![]() Ј©Ј®
Ј©Ј®

ЎҫҪвОцЎҝЈЁ1Ј©°СЕЧОпПЯҪвОцХыАнЈ¬Боy=0ҝЙЗуөГxөДЦөЈ¬ФтҝЙЗуөГAЎўBөДЧшұкЈ»ЈЁ2Ј©УЙAЎўBЎўCөДЧшұкЈ¬ҝЙЗуөГҫӯ№эөгAЎўBЎўCөДЕЧОпПЯҪвОцКҪЈ¬Б¬ҪУBCЎў№эөгPЧчPQЎОyЦбЈ¬Ҫ»BCУЪөгQЈ¬УЙBЎўCөДЧшұкҝЙЗуөГЦұПЯBCөДҪвОцКҪЈ¬ФтҝЙЙиіцPөгЧшұкЈ¬ҙУ¶шұнКҫіцQөгЧшұкЈ¬ФтҝЙЗуөГPQөДіӨЈ¬ҙУ¶шУГPөгЧшұкұнКҫіцЎчPBCөДГж»эЈ¬АыУГ¶юҙОәҜКэөДРФЦКҝЙЗуөГPөгЧшұкәНЎчPBCГж»эөДЧоҙуЦөЈ®
Ўҫҝјөгҫ«ОцЎҝХЖОХ¶юҙОәҜКэөДНјПуәН¶юҙОәҜКэөДРФЦККЗҪвҙрұҫМвөДёщұҫЈ¬РиТӘЦӘөА¶юҙОәҜКэНјПс№ШјьөгЈә1ЎўҝӘҝЪ·ҪПт2Ўў¶ФіЖЦб 3Ўў¶Ҙөг 4ЎўУлxЦбҪ»өг 5ЎўУлyЦбҪ»өгЈ»ФцјхРФЈәөұa>0КұЈ¬¶ФіЖЦбЧуұЯЈ¬yЛжxФцҙу¶шјхРЎЈ»¶ФіЖЦбУТұЯЈ¬yЛжxФцҙу¶шФцҙуЈ»өұa<0КұЈ¬¶ФіЖЦбЧуұЯЈ¬yЛжxФцҙу¶шФцҙ󣻶ԳЖЦбУТұЯЈ¬yЛжxФцҙу¶шјхРЎЈ®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘҫШРОABCDЈ¬өгPОӘBCұЯЙПТ»¶ҜөгЈ¬Б¬ҪУAPЈ¬Ҫ«ПЯ¶ОAPИЖPөгЛіКұХлРэЧӘ90ЎгЈ¬өгAЗЎәГВдФЪЦұПЯCDЙПөгEҙҰЈ®
ЈЁ1Ј©ИзНј1Ј¬өгEФЪПЯ¶ОCDЙПЈ¬ЗуЦӨЈәAD+DE=2ABЈ»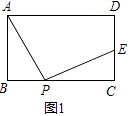
ЈЁ2Ј©ИзНј2Ј¬өгEФЪПЯ¶ОCDөДСУіӨПЯЙПЈ¬ЗТөгDОӘПЯ¶ОCEөДЦРөгЈ¬ФЪПЯ¶ОBDЙПИЎөгFЈ¬Б¬ҪУAFЎўPFЈ¬ИфAF=ABЈ®ЗуЦӨЈәЎПAPF=ЎПADBЈ®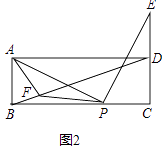
ЈЁ3Ј©ИзНј3Ј¬өгEФЪПЯ¶ОCDЙПЈ¬Б¬ҪУBDЈ¬ИфAB=2Ј¬BDЎОPEЈ¬ФтDE= Ј® ЈЁЦұҪУРҙіцҪб№ыЈ©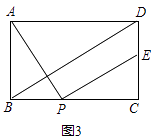
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°СЗт·ЕФЪіӨ·ҪМеЦҪәРДЪЈ¬ЗтөДТ»Іҝ·ЦВ¶іцәРНвЈ¬ЖдҪШГжИзНјЛщКҫЈ¬ТСЦӘEF=CD=16АеГЧЈ¬ФтЗтөД°лҫ¶ОӘАеГЧЈ® 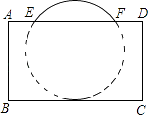
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјұнКҫТ»ФІЦщРОКдЛ®№ЬөДәбҪШГжЈ¬ТхУ°Іҝ·ЦОӘУРЛ®Іҝ·ЦЈ¬Из№ыКдЛ®№ЬөД°лҫ¶ОӘ5cmЈ¬Л®ГжҝнABОӘ8cmЈ¬ФтЛ®өДЧоҙуЙо¶ИCDОӘЈЁ Ј© 
A.4cm
B.3cm
C.2cm
D.1cm
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎСOЦРЈ¬ABОӘЦұҫ¶Ј¬CОӘЎСOЙПТ»өгЈ¬№эөгCЧчЎСOөДЗРПЯЈ¬УлABөДСУіӨПЯПаҪ»УЪөгPЈ¬ИфЎПCAB=27ЎгЈ¬ЗуЎПPөДҙуРЎЈ® 
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЧчНјМв.
(1)ИзНјЈ¬ФЪНјўЩЛщёшөД·ҪёсЦҪЦРЈ¬ГҝёцРЎХэ·ҪРОөДұЯіӨ¶јКЗ1Ј¬ұкәЕОӘўЩўЪўЫөДИэёцИэҪЗРОҫщОӘёсөгИэҪЗРО(¶ҘөгФЪ·ҪёсөД¶ҘөгҙҰ)Ј¬Зл°ҙТӘЗуҪ«НјўЪЦРөДЦё¶ЁНјРО·ЦёоіЙИэёцИэҪЗРОЈ¬К№ЛьГЗУлұкәЕОӘўЩўЪўЫөДИэёцИэҪЗРО·Цұр¶ФУҰИ«өИ(·ЦёоПЯ»ӯіЙКөПЯ);
(2)ИзНјўЫЈ¬ФЪұЯіӨОӘ1ёцөҘО»іӨ¶ИөДРЎХэ·ҪРОЧйіЙөДХэ·ҪРОНшёсЦРЈ¬өг![]() ¶јФЪРЎХэ·ҪРОөД¶ҘөгЙП.
¶јФЪРЎХэ·ҪРОөД¶ҘөгЙП.
ўЩФЪНјЦР»ӯіцУл![]() №ШУЪЦұПЯ
№ШУЪЦұПЯ![]() іЙЦб¶ФіЖөД
іЙЦб¶ФіЖөД![]() ;
;
ўЪЗлФЪЦұПЯ![]() ЙПХТТ»өг
ЙПХТТ»өг![]() Ј¬К№өГ
Ј¬К№өГ![]() өДҫаАлЦ®әНЧоРЎ.
өДҫаАлЦ®әНЧоРЎ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪRtЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬AC=BC=1Ј¬Ҫ«RtЎчABCИЖAөгДжКұХлРэЧӘ30ЎгәуөГөҪRtЎчADEЈ¬өгBҫӯ№эөДВ·ҫ¶ОӘ Ј¬ ФтНјЦРТхУ°Іҝ·ЦөДГж»эКЗ Ј® 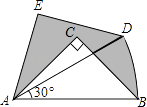
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ТСЦӘ·ҙұИАэәҜКэy= ![]() өДНјПуУлТ»ҙОәҜКэy=ax+bөДНјПуҪ»УЪБҪөгMЈЁ4Ј¬mЈ©әНNЈЁ©Ғ2Ј¬©Ғ8Ј©Ј¬Т»ҙОәҜКэy=ax+bУлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ®
өДНјПуУлТ»ҙОәҜКэy=ax+bөДНјПуҪ»УЪБҪөгMЈЁ4Ј¬mЈ©әНNЈЁ©Ғ2Ј¬©Ғ8Ј©Ј¬Т»ҙОәҜКэy=ax+bУлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ® 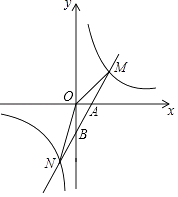
ЈЁ1Ј©ЗуХвБҪёцәҜКэөДҪвОцКҪЈ»
ЈЁ2Ј©ЗуЎчMONөДГж»эЈ»
ЈЁ3Ј©ёщҫЭНјПу»ШҙрЈәөұxИЎәОЦөКұЈ¬·ҙұИАэәҜКэөДЦөҙуУЪТ»ҙОәҜКэөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Ҫ«°лҫ¶ОӘ3cmЈ¬ФІРДҪЗОӘ60ЎгөДЙИРОЦҪЖ¬Ј®AOBФЪЦұПЯlЙППтУТЧчОЮ»¬¶ҜөД№ц¶ҜЦБЙИРОAЎдOЎдBЎдҙҰЈ¬Фт¶ҘөгOҫӯ№эөДВ·ПЯЧЬіӨ cmЈЁҪб№ыұЈБфҰРЈ©Ј®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com