
����Ŀ����ͼ��.
(1)��ͼ����ͼ�������ķ���ֽ�У�ÿ��С�����εı߳�����1�����Ϊ�٢ڢ۵����������ξ�Ϊ���������(�����ڷ���Ķ��㴦)���밴Ҫ��ͼ���е�ָ��ͼ�ηָ�����������Σ�ʹ��������Ϊ�٢ڢ۵����������ηֱ��Ӧȫ��(�ָ�����ʵ��);
(2)��ͼ�ۣ��ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������������У���![]() ����С�����εĶ�����.
����С�����εĶ�����.
����ͼ�л�����![]() ����ֱ��
����ֱ��![]() ����ԳƵ�
����ԳƵ�![]() ;
;
������ֱ��![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() �ľ���֮����С.
�ľ���֮����С.


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ���ᄊ�˶����ϣ����ݲμ��������߳������˶�Ա�ijɼ�����λ��m�������Ƴ����µ�ͳ��ͼ����ͼ��������������Ϣ������������⣺

������ͼ1��a��ֵΪ ��
��������ͳ�Ƶ���������ɼ����ݵ�ƽ��������������λ����
������������������ɼ����ɸߵ���ȷ��9�˽��븴������ֱ��д�������ɼ�Ϊ1.65m���˶�Ա�ܷ���븴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
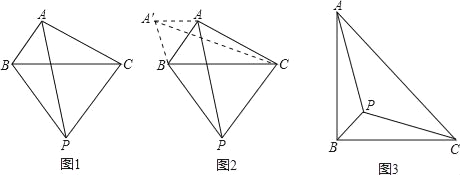
Сΰ��������һ�����⣺��ͼ1������ABC�����С�BAC��һ�����Ա仯�Ľǣ��У�AB=2��AC=4����BCΪ����BC���·����ȱ���PBC����AP�����ֵ��
Сΰ������˼���ģ����ñ任�͵ȱ������ν��ߵ�λ��������ϣ����ķ������Ե�BΪ��ת���Ľ���ABP��ʱ����ת60���õ���A��BC������A��A������A����A��C��ʱ������ɽ⣨��ͼ2����
����ش�AP�����ֵ���� ����
�ο�Сΰͬѧ˼������ķ���������������⣺
��ͼ3������Rt��ABC����AB=4��PΪ��ABC�ڲ�һ�㣬��AP+BP+CP����Сֵ���� ������������Բ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4�������16����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F��![]() ����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��
����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��![]() �ܳ�����СֵΪ
�ܳ�����СֵΪ![]() ����
����![]()

A. 6 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0���� ![]() ������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
������M��������C2��y=mx2��2mx��3m��m��0���Ķ��㣮
��1����A��B��������ꣻ
��2�������ߡ��ڵ����������Ƿ����һ��P��ʹ�á�PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ�����ϣ��Գ���Ϊֱ��x=1��ͼ����3��0�������н����У���ȷ��һ���ǣ� �� 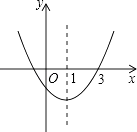
A.abc��0
B.4ac��b2��0
C.a��b+c��0
D.2a+b��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��ѧ����ϣ���ʦ����һ����ͼ���⣺����ͼ����ֱ֪��l��ֱ��l��һ��P.��ֱ�ߺ�Բ����ֱ��PQ��ʹPQ��l�ڵ�Q����

С�����������£�
��1����ֱ��l����ȡ��A����AΪԲ�ģ�AP��Ϊ�뾶������
��2����ֱ��l����ȡ��B����BΪԲ�ģ�BP��Ϊ�뾶������
��3�������ֱ��ڵ�P�͵�M
��4������PM����ֱ��l���ڵ�Q��ֱ��PQ��Ϊ����
��ʦ������С���������ǶԵģ�
��ش�С��������ͼ��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ����������⣺
�߹���ͼ�����Խ��ߵ�����֪�߶ε����Σ�
 ��֪�������߶�a��b��
��֪�������߶�a��b��
����������AMBN,ʹ����Խ��߷ֱ����b��2a��
�߹���ͼ�����Խ��ߵ�����֪�߶ε����Σ�
 ��֪�������߶�a��b��
��֪�������߶�a��b��
����������AMBN,ʹ����Խ��߷ֱ����b��2a��
С�����������£�
��ͼ
(1)��һ���߶�AB����b��
(2)�ֱ���A��BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶��
AB�ij�Ϊ�뾶��
���߶�AB�����¸����������������ཻ��P��Q���㣻
(3)��ֱ��PQ��AB��O�㣻
(4)��O��ΪԲ�ģ��߶�a�ij�Ϊ�뾶������������ֱ��PQ��M��N���㣬����AM��AN��BM��BN�������ı���AMBN�������������.
��ͼ
(1)��һ���߶�AB����b��
(2)�ֱ���A��BΪԲ�ģ�����![]() AB�ij�Ϊ�뾶��
AB�ij�Ϊ�뾶��
���߶�AB�����¸����������������ཻ��P��Q���㣻
(3)��ֱ��PQ��AB��O�㣻
(4)��O��ΪԲ�ģ��߶�a�ij�Ϊ�뾶������������ֱ��PQ��M��N���㣬����AM��AN��BM��BN�������ı���AMBN�������������.
��ʦ˵����С����������ȷ����
������߹���ͼ��������AMBN��������_______________________________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺����2��2+�� ![]() ��1��0��
��1��0�� ![]() ����
���� ![]() ����1
����1
��2���� ![]() ��
�� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com