
【题目】如图,四边形ABCD是正方形,△EBC是等边三角形. 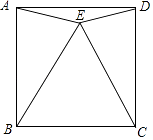
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
【答案】
(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
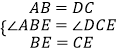 ,
,
∴△ABE≌△DCE(SAS)
(2)∵BA=BE,∠ABE=30°,
∴∠BAE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
【解析】(1)根据正方形、等边三角形的性质,可以得到AB=BE=CE=CD,∠ABE=∠DCE=30°,由此即可证明;(2)只要证明∠EAD=∠ADE=15°,即可解决问题;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= . 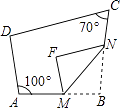
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图BE//CF,BE、CF分别平分∠ABC和∠BCD, 求证:AB//CD

证明:∵ BE、CF分别平分∠ABC和∠BCD(已知)
∴ ∠1=![]() ∠ ∠2=
∠ ∠2=![]() ∠ ( )
∠ ( )
∵ BE//CF( )
∴ ∠1=∠2( )
∴ ![]() ∠ABC=
∠ABC=![]() ∠BCD
∠BCD
即∠ABC=∠BCD
∴ AB//CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=______秒(s)时,点P、Q、C、D构成平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件是:①AB=DE;②AC=DF;③AC∥DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取信息的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式和图中a的值分别是( )

A. 抽样调查,24 B. 普查,24 C. 抽样调查,26 D. 普查,26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF. 
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了了解2018年初中毕业生毕业后的去向,对部分九年级学生进行了抽样调查,就九年级学生的四种去向(A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他)进行数据统计,并绘制了两幅不完整的统计图(如图①②)请问:

(1)本次共调查了_ 名初中毕业生;
(2)请计算出本次抽样调查中,读职业高中的人数和所占百分比,并将两幅统计图中不完整的部分补充完整;
(3)若该县2018年九年级毕业生共有![]() 人,请估计该县今年九年级毕业生读职业高中的学生人数.
人,请估计该县今年九年级毕业生读职业高中的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com