
【题目】甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
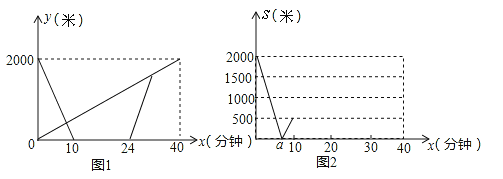
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
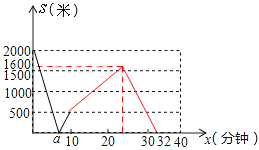
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
【答案】 (1) y1=﹣200x+2000。
(2) s=﹣150x+4800。
(3)详见解析
【解析】
(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得:
![]() ,解得:
,解得:![]() 。
。
∴y1=﹣200x+2000。
(2)由题意,得小明的速度为:2000÷40=50米/分,小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:s=24×50=1200;32分钟时S=0。
设s与x之间的函数关系式为:s=kx+b1,由题意,得
![]() ,解得:
,解得:![]() 。
。
∴s=﹣150x+4800。
(3)由题意,得a=2000÷(200+50)=8分钟,
当x=24时,s=1200;当x=32时,S=0。
故描出相应的点就可以补全图象如图:


科目:初中数学 来源: 题型:
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
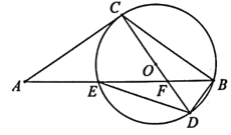
(1)求⊙O的直径.
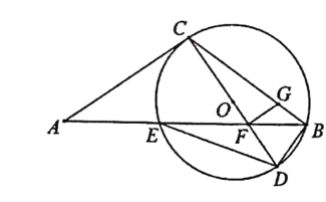
(2)过点F作FG⊥CD交BC于点G,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
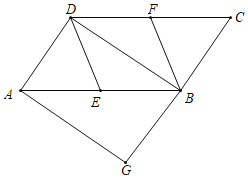
【题目】如图,在平行四边形ABCD中,点E、F分别为边AB、CD的中点,BD是平行四边形ABCD的对角线,AG∥BD交CB的延长线于点G
(1)求证:四边形BEDF是平行四边形;
(2)若AE=DE,则四边形AGBD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=ax+b与双曲线![]() 交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
(1)①求k的值和点C的坐标;②求直线l的表达式;
(2)过点B作y轴的垂线与直线AC交于点D,经过点C的直线与直线BD交于点E.若30°≤∠CED≤45°,直接写出点E的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,摸到蓝球的概率为 ;
(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,求至少有1次摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
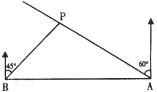
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与
OD的延长线交于点P,PC、AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
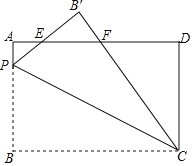
【题目】如图,矩形ABCD中,AB=5,BC=8,点P在AB上,AP=1.将矩形ABCD沿CP折叠,点B落在点B'处.B'P、B′C分别与AD交于点E、F,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
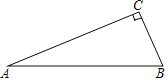
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com