
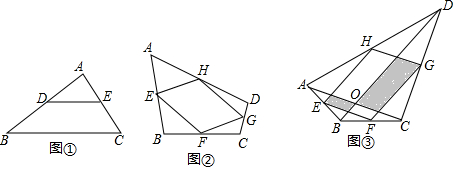
分析 【探究】利用三角形的中位线定理可得出HG=EF、EF∥GH,继而可判断出四边形EFGH的形状;
【应用】(1)同【探究】的方法判断出EF=$\frac{1}{2}$AC,即可判断出EF=FG,即可得出结论;
(2)先判断出S△BCD=4S△CFG,同理:S△ABD=4S△AEH,进而得出S四边形EFGH=$\frac{5}{2}$,再判断出OM=ON,进而得出S阴影=$\frac{1}{2}$S四边形EFGH即可.
解答 解:【探究】平行四边形.
理由:如图1,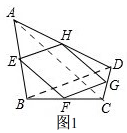 连接AC,
连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理HG∥AC,HG=$\frac{1}{2}$AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形.
【应用】(1)添加AC=BD,
理由:连接AC,BD,同(1)知,EF=$\frac{1}{2}$AC,
同【探究】的方法得,FG=$\frac{1}{2}$BD,
∵AC=BD,
∴EF=FG,
∵四边形EFGH是平行四边形,
∴?EFGH是菱形;
故答案为AC=BD;
(2)如图2, 由【探究】得,四边形EFGH是平行四边形,
由【探究】得,四边形EFGH是平行四边形,
∵F,G是BC,CD的中点,
∴FG∥BD,FG=$\frac{1}{2}$BD,
∴△CFG∽△CBD,
∴$\frac{{S}_{△CFG}}{{S}_{△BCD}}=\frac{1}{4}$,
∴S△BCD=4S△CFG,
同理:S△ABD=4S△AEH,
∵四边形ABCD面积为5,
∴S△BCD+S△ABD=5,
∴S△CFG+S△AEH=$\frac{5}{4}$,
同理:S△DHG+S△BEF=$\frac{5}{4}$,
∴S四边形EFGH=S四边形ABCD-(S△CFG+S△AEH+S△DHG+S△BEF)=5-$\frac{5}{2}$=$\frac{5}{2}$,
设AC与FG,EH相交于M,N,EF与BD相交于P,
∵FG∥BD,FG=$\frac{1}{2}$BD,
∴CM=OM=$\frac{1}{2}$OC,
同理:AN=ON=$\frac{1}{2}$OA,
∵OA=OC,
∴OM=ON,
易知,四边形ENOP,FMOP是平行四边形,
∴S阴影=$\frac{1}{2}$S四边形EFGH=$\frac{5}{4}$,
故答案为$\frac{5}{4}$.
点评 此题是四边形综合题,主要考查了三角形的中位线定理,平行四边形的判定,菱形的判定,相似三角形的判定和性质,解【探究】的关键是判断出HG∥AC,HG=$\frac{1}{2}$AC,解【应用】的关键是判断出S四边形EFGH=$\frac{5}{2}$,是一道基础题目.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
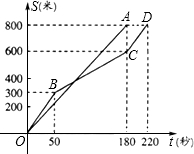 在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )
在今年我县初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小英和小西所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,如图,下列说法正确的是( )| A. | 小英的速度随时间的增大而增大 | |
| B. | 小西的平均速度比小英的平均速度大 | |
| C. | 在起跑后180秒时,两人相遇 | |
| D. | 在起跑后50秒时,小西在小英的前面 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
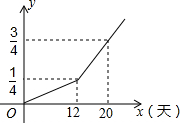 甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.
甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{7x+7=y}\\{9(x-1)=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x+7=y}\\{9(x+1)=y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x-7=y}\\{9(x-1)=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x-7=y}\\{9(x+1)=y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB的中垂线交AB于点,交BC于点D,若△ADC的周长为17cm,AC=5cm,则BC的长为( )
如图,在△ABC中,AB的中垂线交AB于点,交BC于点D,若△ADC的周长为17cm,AC=5cm,则BC的长为( )| A. | 7cm | B. | 10cm | C. | 12cm | D. | 22cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发4.68小时候再与轿车相遇(结果精确到0.01).
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发4.68小时候再与轿车相遇(结果精确到0.01).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com