练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD各顶点的坐标分别为A（2，6），B（4，2），C（6，2），D（6，4），

    ①在第一象限内，画出以原点为位似中心，相似比为的位似图形A1B1C1D1；

    ②将四边形A1B1C1D1向右平移5个单位长度，再向上平移4个单位长度，并写出各点坐标．

    【答案】①见解析；②见解析，A2（6，7）、B2（7，5）、C2（8，5）、D2（8，6）

    【解析】

    ①根据位似变换的概念分别作出四个顶点的对应点，再首尾顺次连接即可得；

    ②根据平移变换的概念作出变换后的对应点，再首尾顺次连接即可得．

    解：①如图所示，四边形A1B1C1D1即为所求．

    ②如图所示，四边形A2B2C2D2即为所求，其中A2（6，7）、B2（7，5）、C2（8，5）、D2（8，6）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】参照学习函数的过程与方法，探究函数的图象与性质．因为，即，所以我们对比函数来探究．

    列表：

    …

    -4

    -3

    -2

    -1

    2

    3

    4

    …

    …

    1

    2

    4

    -4

    -1

    …

    …

    2

    3

    5

    -3

    -1

    0

    …

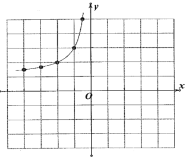
    描点：在平面直角坐标系中，以自变量的取值为横坐标，以相应的函数值为纵坐标，描出相应的点，如图所示：

    （1）①请补全表格，计算__________．

    ②请补全图形，用一条光滑曲线顺次连接起来；

    （2）观察图象并分析表格，回答下列问题：

    ①当时，随的增大而__________；（填“增大”或“减小”）

    ②的图象是由的图象向__________平移__________个单位而得到；

    ③图象关于点__________中心对称．（填点的坐标）

    （3）结合函数图象，当时，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

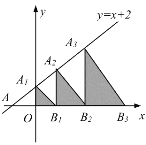
    【题目】如图，在平面直角坐标系中，直线交轴于点，交轴于点，若图中阴影部分的三角形都是等腰直角三角形，则从左往右数第5个阴影三角形的面积是_____，第2019个阴影三角形的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

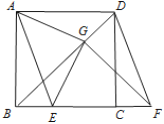
    【题目】如图，是正方形的对角线，，边在其所在直线上向右平移，将通过平移得到的线段记为，连结，，并过点作，垂足为，连接和，在平移变换过程中，设的面积为，，则的最大值是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

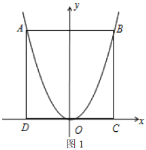
    【题目】矩形对角线的四等分点叫做矩形的奇特点．如图，在平面直角坐标系中，点，为抛物线上的两个动点（在的左侧），且轴，以为边画矩形，原点在边上．

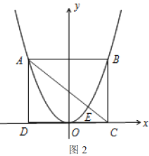
    （1）如图1，当矩形为正方形时，求该矩形在第一象限内的奇特点的坐标．

    （2）如图2，在点，的运动过程中，连结交抛物线于点．

    ①求证：点为矩形的奇特点；

    ②连结，若，抛物线上的点为矩形的另一奇特点，求经过，，三点的圆的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线C：y＝与直线l：y＝kx+b相交于点A，B，直线l与y轴交于点P．

    （1）当k＝0时，求的值；

    （2）点M是抛物线上的动点，过点M作MG⊥直线l于点G，当k＝0时，求的值；

    （3）点M是抛物线上的动点，过点M作MG∥y轴交直线l于点G，当k＝2时，求证：不论b为何实数，的值为定值，并求定值；

    （4）若将（2）的抛物线改为“y＝ax2”，其他条件不变，则的值还为定值吗？若是，请求出定值；若不是，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax2﹣10ax+c经过点C，顶点M在直线BC上．

    （1）证明四边形ABCD是菱形，并求点D的坐标；

    （2）求抛物线的对称轴和函数表达式；

    （3）在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

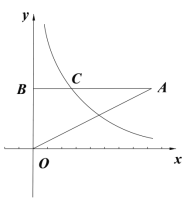
    【题目】如图，在平面直角坐标系中，点A在第一象限，BA⊥y轴于点B，反比例函数y=（x＞0）的图象与线段AB相交于点C，且C是线段AB的中点，若△OAB的面积为3，则k的值为( )

    A.B.1C.2D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

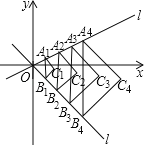
    【题目】如图，在平面直角坐标系中，△A1B1C1，△A2B2C2，△A3B3C3，…，△AnBnCn均为等腰直角三角形，且∠C1＝∠C2＝∠C3＝…＝∠Cn＝90°，点A1，A2，A3，…，An和点B1，B2，B3，…，Bn分别在正比例函数y＝x和y＝﹣x的图象上，且点A1，A2，A3，…，An的横坐标分别为1，2，3…n，线段A1B1，A2B2，A3B3，…，AnBn均与y轴平行．按照图中所反映的规律，则△AnBnCn的顶点Cn的坐标是____．（其中n为正整数）

    查看答案和解析>>

    同步练习册答案