
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКyЃН![]() гыжБЯпlЃКyЃНkx+bЯрНЛгкЕуAЃЌBЃЌжБЯпlгыyжсНЛгкЕуPЃЎ
гыжБЯпlЃКyЃНkx+bЯрНЛгкЕуAЃЌBЃЌжБЯпlгыyжсНЛгкЕуPЃЎ
ЃЈ1ЃЉЕБkЃН0ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕуMЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуMзїMGЁЭжБЯпlгкЕуGЃЌЕБkЃН0ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЕуMЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуMзїMGЁЮyжсНЛжБЯпlгкЕуGЃЌЕБkЃН2ЪБЃЌЧѓжЄЃКВЛТлbЮЊКЮЪЕЪ§ЃЌ![]() ЕФжЕЮЊЖЈжЕЃЌВЂЧѓЖЈжЕЃЛ
ЕФжЕЮЊЖЈжЕЃЌВЂЧѓЖЈжЕЃЛ
ЃЈ4ЃЉШєНЋЃЈ2ЃЉЕФХзЮяЯпИФЮЊЁАyЃНax2ЁБЃЌЦфЫћЬѕМўВЛБфЃЌдђ![]() ЕФжЕЛЙЮЊЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіЖЈжЕЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЎ
ЕФжЕЛЙЮЊЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіЖЈжЕЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌЖЈжЕЮЊ
ЃЛЃЈ3ЃЉжЄУїМћНтЮіЃЌЖЈжЕЮЊ![]() ЃЛЃЈ4ЃЉЮЊЖЈжЕЃЌ
ЃЛЃЈ4ЃЉЮЊЖЈжЕЃЌ![]() ЃН|a|ЃЎ
ЃН|a|ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіХзЮяЯпгыжБЯпЕФНЛЕузјБъЃЌгЩСНЕуОрРыЙЋЪНЧѓЕУЯпЖЮГЄЖШЃЌБуПЩМЦЫу![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩшMЕуЕФзјБъЃЌЧѓГіХзЮяЯпгыжБЯпЕФНЛЕузјБъЃЌгУСНЕуОрРыЙЋЪНЧѓЕУЯпЖЮГЄЖШЃЌНјЖјМЦЫуНсЙћЃЛ
ЃЈ3ЃЉЩшMЕуЕФзјБъЃЌЧѓГіХзЮяЯпгыжБЯпЕФНЛЕузјБъЃЌгУСНЕуОрРыЙЋЪНЧѓЕУЯпЖЮГЄЖШЃЌНјЖјМЦЫуНсЙћЃЛ
ЃЈ4ЃЉвРееЧАУцЕФНтЗЈНјааМЦЫуБуПЩЃЎ
НтЃКЃЈ1ЃЉЕБkЃН0ЪБЃЌyЃНbЃЌ
ЁрOPЃН|b|ЃЌ
Ёп![]() ЃНbЃЌ
ЃНbЃЌ
ЁрxЃНЁР![]() bЃЌ
bЃЌ
ЁрAЃЈЉ![]() bЃЌbЃЉЃЌBЃЈ
bЃЌbЃЉЃЌBЃЈ![]() bЃЌbЃЉЃЌ
bЃЌbЃЉЃЌ
ЁрABЃН2![]() bЃЌ
bЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБkЃН0ЪБЃЌyЃНbЃЌ
ЩшMЃЈxЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпMGЁЭжБЯпlЃЌ
ЁрMGЃН|![]() Љb|ЃЌ
Љb|ЃЌ
ЁпAЃЈЉ![]() bЃЌ0ЃЉЃЌBЃЈ
bЃЌ0ЃЉЃЌBЃЈ![]() bЃЌ0ЃЉЃЌ
bЃЌ0ЃЉЃЌ
ЁрGAЃН|x+![]() b|ЃЌGBЃН|xЉ
b|ЃЌGBЃН|xЉ![]() b|ЃЌ
b|ЃЌ
Ёр![]() ЃН
ЃН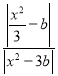 ЃН
ЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБkЃН2ЪБЃЌyЃН2x+bЃЌ
ЩшMЃЈxЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпMGЁЮyжсЃЌ
ЁрGЃЈxЃЌ2x+bЃЉЃЌ
ЁрGMЃН|![]() Љ2xЉb|ЃН
Љ2xЉb|ЃН![]() ЃЌ
ЃЌ
НтЗНГЬзщ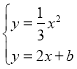 ЕУЃЌ
ЕУЃЌ
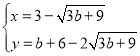 Лђ
Лђ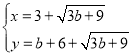
AЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌBЃЈ3+
ЃЉЃЌBЃЈ3+![]() ЃЌb+6+
ЃЌb+6+![]() ЃЉЃЌ
ЃЉЃЌ
ЁрGAЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
GBЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрGAGBЃН5|x2Љ6xЉ3b|ЃЌ
Ёр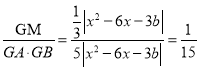 ЃЛ
ЃЛ
ЃЈ4ЃЉЪЧЖЈжЕЃЎ
ЕБkЃН0ЪБЃЌyЃНbЃЌ
ЩшMЃЈxЃЌax2ЃЉЃЌ
ЁпMGЁЭжБЯпlЃЌ
ЁрMGЃН|ax2Љb|ЃЌ
НтЗНГЬзщ![]() ЕУЃЌ
ЕУЃЌ
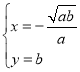 Лђ
Лђ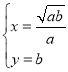 ЃЌ
ЃЌ
ЁпAЃЈЉ![]() ЃЌbЃЉЃЌBЃЈ
ЃЌbЃЉЃЌBЃЈ![]() ЃЌbЃЉЃЌ
ЃЌbЃЉЃЌ
ЁрGAЃН|x+![]() |ЃЌGBЃН|xЉ
|ЃЌGBЃН|xЉ![]() |ЃЌ
|ЃЌ
Ёр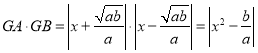 ЃН
ЃН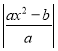
Ёр![]() ЃН|a|ЮЊЖЈжЕЃЎ
ЃН|a|ЮЊЖЈжЕЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпy=Љx+7a+1гыжБЯпy=2xЉ2a+4ЭЌЪБОЙ§ЕуPЃЌЕуQЪЧвдMЃЈ0ЃЌЉ1ЃЉЮЊдВаФЃЌMOЮЊАыОЖЕФдВЩЯЕФвЛИіЖЏЕуЃЌдђЯпЖЮPQЕФзюаЁжЕЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЕМљВйзї
ШчЭМ1ЃЌНЋОиаЮжНЦЌ![]() биЖдНЧЯп
биЖдНЧЯп![]() ЗелЃЌЪЙЕу
ЗелЃЌЪЙЕу![]() ТфдкОиаЮ
ТфдкОиаЮ![]() ЫљдкЦНУцФкЃЌ
ЫљдкЦНУцФкЃЌ![]() КЭ
КЭ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
НтОіЮЪЬт
ЃЈ1ЃЉдкЭМ1жаЃЌЂй![]() КЭ
КЭ![]() ЕФЮЛжУЙиЯЕЮЊ__________ЃЛЂкНЋ
ЕФЮЛжУЙиЯЕЮЊ__________ЃЛЂкНЋ![]() МєЯТКѓеЙПЊЃЌЕУЕНЕФЭМаЮЪЧ_____ЃЛ
МєЯТКѓеЙПЊЃЌЕУЕНЕФЭМаЮЪЧ_____ЃЛ
ЃЈ2ЃЉШєЭМ1жаЕФОиаЮБфЮЊЦНааЫФБпаЮЪБ![]() ЃЌШчЭМ2ЫљЪОЃЌНсТлЂйКЭНсТлЂкЪЧЗёГЩСЂЃЌШєГЩСЂЃЌЧыЬєбЁЦфжаЕФвЛИіНсТлМгвджЄУїЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЌШчЭМ2ЫљЪОЃЌНсТлЂйКЭНсТлЂкЪЧЗёГЩСЂЃЌШєГЩСЂЃЌЧыЬєбЁЦфжаЕФвЛИіНсТлМгвджЄУїЃЌШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЭиеЙгІгУ
ЃЈ3ЃЉаЁКьбиЖдНЧЯпелЕўвЛеХОиаЮжНЦЌЃЌЗЂЯжЫљЕУЭМаЮЪЧжсЖдГЦЭМаЮЃЌбиЖдГЦжсдйДЮелЕўКѓЃЌЕУЕНЕФШдЪЧжсЖдГЦЭМаЮЃЌдђаЁКьелЕўЕФОиаЮжНЦЌЕФГЄПэжЎБШЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЕЭЬМГіааЃЌТЬЩЋГіааЁБЃЌздааГЕж№НЅГЩЮЊШЫУЧЯВАЎЕФНЛЭЈЙЄОпЃЌФўВЈФГдЫЖЏЩЬГЧЕФздааГЕЯњЪлСПзд2016ФъЦ№ж№ФъдіМгЃЌОнЭГМЦИУЩЬГЧ2016ФъЯњЪлздааГЕ768СОЃЌ2018ФъЯњЪлСЫ1200СОЃЎ
ЃЈ1ЃЉШєИУЩЬГЧНќЫФФъЕФздааГЕЯњЪлСПФъЦНОљдіГЄТЪЯрЭЌЃЌЧыФудЄЙРЃКИУЩЬГЧ2019ФъДѓИХФмТєГіЖрЩйСОздааГЕЃП
ЃЈ2ЃЉПМТЧЕНздааГЕашЧѓЕФВЛЖЯдіМгЃЌБОдТИУЩЬГЁзМБИЭЖШы3ЭђдЊдйЙКНјвЛХњСНжжЙцИёЕФздааГЕЃЌвбжЊ![]() аЭГЕЕФНјМлЮЊ500дЊ/СОЃЌЪлМлЮЊ700дЊ/СОЃЌ
аЭГЕЕФНјМлЮЊ500дЊ/СОЃЌЪлМлЮЊ700дЊ/СОЃЌ![]() аЭГЕЕФНјМлЮЊ1000дЊ/СОЃЌЪлМлЮЊ1300дЊ/СОЃЎИљОнЯњЪлОбщЃЌ
аЭГЕЕФНјМлЮЊ1000дЊ/СОЃЌЪлМлЮЊ1300дЊ/СОЃЎИљОнЯњЪлОбщЃЌ![]() аЭГЕВЛЩйгк
аЭГЕВЛЩйгк![]() аЭГЕЕФ2БЖЃЌЕЋВЛГЌЙ§
аЭГЕЕФ2БЖЃЌЕЋВЛГЌЙ§![]() аЭГЕЕФ3.2БЖЃЌМйЩшЫљНјГЕСОШЋВПЪлЭъЃЌЮЊЪЙЕУРћШѓзюДѓЃЌИУЩЬГЁИУШчКЮНјЛѕЃП
аЭГЕЕФ3.2БЖЃЌМйЩшЫљНјГЕСОШЋВПЪлЭъЃЌЮЊЪЙЕУРћШѓзюДѓЃЌИУЩЬГЁИУШчКЮНјЛѕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
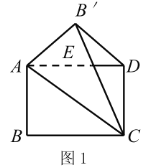
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDИїЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ2ЃЌ6ЃЉЃЌBЃЈ4ЃЌ2ЃЉЃЌCЃЈ6ЃЌ2ЃЉЃЌDЃЈ6ЃЌ4ЃЉЃЌ
ЂйдкЕквЛЯѓЯоФкЃЌЛГівддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ![]() ЕФЮЛЫЦЭМаЮA1B1C1D1ЃЛ
ЕФЮЛЫЦЭМаЮA1B1C1D1ЃЛ
ЂкНЋЫФБпаЮA1B1C1D1ЯђгвЦНвЦ5ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ4ИіЕЅЮЛГЄЖШЃЌВЂаДГіИїЕузјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
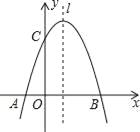
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=![]() +mx+3гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ
+mx+3гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ
ЃЈ1ЃЉЧѓmЕФжЕМАХзЮяЯпЕФЖЅЕузјБъЃЎ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЖдГЦжсlЩЯЕФвЛИіЖЏЕуЃЌЕБPA+PCЕФжЕзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНтЃК
дВЪЧзюЭъУРЕФЭМаЮЃЌЫќОпгавЛаЉЬиЪтЕФаджЪЃКЭЌЛЁЛђЕШЛЁЫљЖдЕФдВжмНЧЯрЕШЃЌвЛЬѕЛЁЫљЖдЕФдВжмНЧЕШгкетЬѕЛЁЫљЖдЕФдВаФНЧЕФвЛАыЁЁЃЛЯШЙЙдьЁАИЈжњдВЁБЃЌдйРћгУдВЕФаджЪНЋЮЪЬтНјаазЊЛЏЃЌЭљЭљФмЛЏвўЮЊЯдЁЂЛЏФбЮЊвзЃЎ

НтОіЮЪЬтЃК
ШчЭМЃЌЕу![]() гыЕу
гыЕу![]() ЕФзјБъЗжБ№ЪЧ
ЕФзјБъЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЪЙ![]() ЕФЕу
ЕФЕу![]() га_________ИіЃЛ
га_________ИіЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЕФИКАыжсЩЯЃЌЧв
ЕФИКАыжсЩЯЃЌЧв![]() ЃЌЧѓТњзуЬѕМўЕФЕу
ЃЌЧѓТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊШёНЧЪБЃЌЩш
ЮЊШёНЧЪБЃЌЩш![]() ЃЌШєЕу
ЃЌШєЕу![]() дк
дк![]() жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу
жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу![]() га4ИіЃЌЧѓ
га4ИіЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
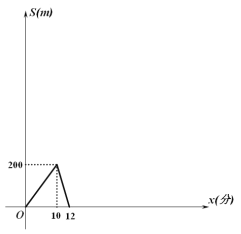
ЁОЬтФПЁПШЋУёНЁЩэЕФНёЬьЃЌЩЂВНдЫЖЏЪЧДѓжкЯВЛЖЕФЛюЖЏЯюФПЁЃМвзЁЭЌвЛаЁЧјЕФМзввСНШЫУПЬьЖМдкЭЌвЛЬѕШчЭМ1ЕФбєЙтзпЕРЩЯРДЛиЩЂВНЃЎФГЬьЃЌМзввСНШЫЭЌЪБДгДѓЕРЕФAЖЫвдИїздЕФЫйЖШдШЫйдкДѓЕРЩЯЩЂВННЁЩэЃЌВНаавЛЖЮЪБМфКѓЃЌМзНгЕНЯћЯЂгаЭЌЪТдкГіЗЂЕиЕШЫћЩЬСПЪТЮёЃЈМзЪеЯћЯЂЕФЪБМфКіТдВЛМЦЃЉЃЌгкЪЧМзАДдЫйЖШЗЕЛиЃЌгіМћввКѓгУдРДЕФ2БЖЫйЖШХмВНЧАЭљЃЌДЫЪБввШдАДдМЦЛЎМЬајЩЂВНдЫЖЏЃЌ4ЗжжгКѓМзНсЪјСЫЬИЛАЃЌМЬајАДдЫйЖШдЫЖЏЃЎЭМ2ЪЧМзввСНШЫжЎМфЕФОрРыSЃЈmЃЉгыЫћУЧГіЗЂКѓЕФЪБМфxЃЈЗжЃЉжЎМфКЏЪ§ЙиЯЕЕФВПЗжЭМЯёЃЌвбжЊМзВНааЫйЖШБШввПьЃЎ
ЃЈ1ЃЉгЩЭМЯёПЩжЊЃЌМзЕФЫйЖШЮЊ___ ___m/ЗжЃЛввЕФЫйЖШЮЊ_____m/ЗжЃЎ
ЃЈ2ЃЉШєМзДІРэЭъЪТЧщМЬајАДдЫйЖШЩЂВНЃЌдйДЮгіЕНввКѓСНШЫЩдзїЗХЫЩКѓОЭИїздЛиМвЃЌИљОнвбгааХЯЂЃЌОЭМзввСНШЫвЛЦ№ЩЂВНЕНЕкЖўДЮЯргіЕФЙ§ГЬЃЌЧыдкЭМ2жаВЙШЋКЏЪ§ЭМЯёЃЌВЂаДГіЫљВЙЕФЭМЯёжаЕФSгыxЕФКЏЪ§ЙиЯЕЪНМАxЕФШЁжЕЗЖЮЇЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЮФОпЩЬЕъЯњЪлбЇЯАгУЦЗЃЌвбжЊФГЦЗХЦИжБЪЕФНјМлЪЧ20дЊЃЌЯњЪлЙ§ГЬЗЂЯжЃЌУПдТЯњСПyжЇгыЯњЪлЕЅМлxдЊЃЈxЮЊе§ећЪ§ЃЉжЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЌЧвУПжЇИжБЪЕФЪлМлВЛЕЭгкНјМлЃЌвВВЛИпгк35дЊЃЌЯТБэЪЧyгыxжЎМфЕФЖдгІЪ§ОнЃК
ЯњЪлЕЅМлxЃЈдЊЃЉ | Ё | 22 | 24 | 30 | Ё |
дТЯњСПyЃЈжЛЃЉ | Ё | 92 | 84 | 60 | Ё |
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНВЂжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇ.
ЃЈ2ЃЉУПжЇИжБЪЕФЪлМлЖЈЮЊЖрЩйдЊЪБЃЌдТЯњЪлРћШѓЧЁЮЊ600дЊЃП
ЃЈ3ЃЉУПжЇИжБЪЕФЪлМлЖЈЮЊЖрЩйдЊЪБПЩЪЙдТЯњЪлРћШѓзюДѓЃПзюДѓЕФдТРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com