
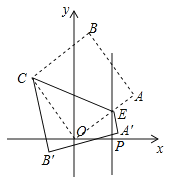
【题目】如图,在平面直角坐标系中,坐标原点O是正方形OABC的一个顶点,已知点B坐标为(1,7),过点P(a,0)(a>0)作PE⊥x轴,与边OA交于点E(异于点O、A),将四边形ABCE沿CE翻折,点A′、B′分别是点A、B的对应点,若点A′恰好落在直线PE上,则a的值等于( )
A.![]() B.
B.![]() C.2D.3
C.2D.3
【答案】C
【解析】
解:当点A′恰好落在直线PE上,如图所示,连接OB、AC交于点D,过点D、A作x轴的垂线,垂足分别为Q、N,设CB′交x轴于M,则CM∥QD∥AN.∵四边形OABC是正方形,∴OD=BD,OB⊥AC.∵O(0,0),B(1,7),∴D(![]() ,
,![]() ).由勾股定理得:OB=
).由勾股定理得:OB=![]() =
=![]() =
=![]() .∵△ABO是等腰直角三角形,∴AB=AO=5.∵DQ是梯形CMNA的中位线,∴CM+AN=2DQ=7.∵∠COA=90°,∴∠COM+∠AON=90°.∵∠CMO=90°,∴∠COM+∠MCO=90°,∴∠AON=∠MCO.∵四边形OABC是正方形,∴OA=OC.∵∠CMO=∠ONA=90°,∴△CMO≌△ONA,∴ON=CM,∴ON+AN=7.设AN=x,则ON=7﹣x.在Rt△AON中,由勾股定理得:x2+(7﹣x)2=52,解得:x=3或4.当x=4时,CM=3,此时点B在第二象限,不符合题意,∴x=3,∴OM=3.∵A′B′=PM=5,∴OP=a=2.故选C.
.∵△ABO是等腰直角三角形,∴AB=AO=5.∵DQ是梯形CMNA的中位线,∴CM+AN=2DQ=7.∵∠COA=90°,∴∠COM+∠AON=90°.∵∠CMO=90°,∴∠COM+∠MCO=90°,∴∠AON=∠MCO.∵四边形OABC是正方形,∴OA=OC.∵∠CMO=∠ONA=90°,∴△CMO≌△ONA,∴ON=CM,∴ON+AN=7.设AN=x,则ON=7﹣x.在Rt△AON中,由勾股定理得:x2+(7﹣x)2=52,解得:x=3或4.当x=4时,CM=3,此时点B在第二象限,不符合题意,∴x=3,∴OM=3.∵A′B′=PM=5,∴OP=a=2.故选C.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴负半轴相交于点A,与y轴正半轴相交于点B,
与x轴负半轴相交于点A,与y轴正半轴相交于点B,![]() ,直线l过A、B两点,点D为线段AB上一动点,过点D作
,直线l过A、B两点,点D为线段AB上一动点,过点D作![]() 轴于点C,交抛物线于点E.
轴于点C,交抛物线于点E.
(1)求抛物线的解析式;
(2)若抛物线与x轴正半轴交于点F,设点D的横坐标为x,四边形FAEB的面积为S,请写出S与x的函数关系式,并判断S是否存在最大值,如果存在,求出这个最大值;并写出此时点E的坐标;如果不存在,请说明理由.
(3)连接BE,是否存在点D,使得![]() 和
和![]() 相似?若存在,求出点D的坐标;若不存在,说明理由.
相似?若存在,求出点D的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上.

(1)从中随机抽出一张牌,牌面数字是奇数的概率是 ;
(2)从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
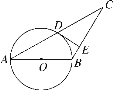
【题目】如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是( )
A.3B.4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
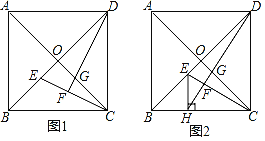
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
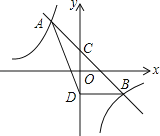
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
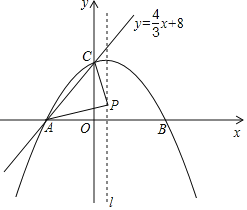
【题目】如图,在平面直角坐标系中,直线AC:y=![]() x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2
x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2![]() ,则抛物线的解析式为_____.
,则抛物线的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
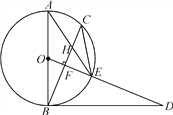
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
求证:(1)BD是⊙O的切线;
(2)若EH=2,AH=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意一点![]() 我们定义:当
我们定义:当![]() 为常数,且
为常数,且![]() 时,点
时,点![]() 为点
为点![]() 的“
的“![]() 对应点”.
对应点”.
(1)点![]() 的“
的“![]() 对应点”
对应点”![]() 的坐标为 ;若点
的坐标为 ;若点![]() 的“
的“![]() 对应点”
对应点”![]() 的坐标为
的坐标为![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,则点
,则点![]() 的横坐标
的横坐标![]() ;
;
(2)若点![]() 的“
的“![]() 对应点”
对应点”![]() 在第一、三象限的角平分线(原点除外)上,求
在第一、三象限的角平分线(原点除外)上,求![]() 值;
值;
(3)若点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 的“
的“![]() 对应点”为
对应点”为![]() 点,且
点,且![]() ,求
,求![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com