
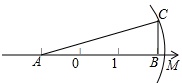
 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )| A. | ($\sqrt{5}$-1,0) | B. | (2,0) | C. | ($\sqrt{10}$-1,0) | D. | ($\sqrt{10}$,0) |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
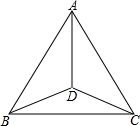 如图,点D是△ABC内部一点,AD平分∠BAC.
如图,点D是△ABC内部一点,AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
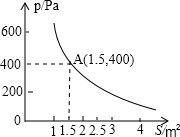 某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示
某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
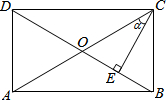 如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com