
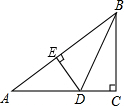
 如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是
如图,在直角三角形ABC中,∠C=90°,BC=6cm,AC=8cm,按图中方法将△BCD沿BD折叠,使点C落在AB边的E点,那么△ADE的面积是| AC2+BC2 |
| 82+62 |
| 1 |
| 2 |
| 1 |
| 2 |


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点A(a,1)、B(-1,b)都在双曲线y=-
如图,点A(a,1)、B(-1,b)都在双曲线y=-| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
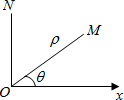 在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为
在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥OX,且点N到极点O的距离为4个单位长度,则点N的极坐标可表示为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com