
【题目】某公司在A,B两地分别有同型号的机器17台和15台,目前需要把这些机器中的18台运往甲地,14台运往乙地.从A,B两地运往甲,乙两地的费用如表:
甲地(元/台) | 乙地(元/台) | |
A地 | 600 | 500 |
B地 | 400 | 800 |
(1)设从A地运往甲地x台,则从A地运往乙地 台,从B地运往乙地 台.(结果用x的代数式表示,且代数式化到最简)
(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
(3)能否有一种运送方案比(2)中方案的总运费低?如果有,直接写出运送方案及所需运费;如果没有,请说明理由.
【答案】(1)17﹣x,x﹣3;(2)当运送总费用为15800元时,从A地运往甲地5台,运往乙地12台;从B地运往甲地13台,运往乙地2台;(3)从A地运往甲地3台,运往乙地14台;从B地运往甲地15台,运往乙地0台.最低运费为14800元.
【解析】
(1)按题目的数量关系计算即可得答案.
(2)把每种情况的运费与相应的数量相乘,再把积相加,即为总运费,列得方程并求解.
(3)设总运费为y,可列得y关于x的函数关系式,再根据一次函数性质和x的取值范围,即能求得运费最小值.
解:(1)∵A地有17台机器,运往甲地x台
∴剩(17﹣x)台运往乙地
∵需运14台机器到乙地,A地已运(17﹣x)台过来
∴剩下需由B地运来的台数为:14﹣(17﹣x)=x﹣3
故答案为:17﹣x;x﹣3
(2)依题意得:600x+500(17﹣x)+400(18﹣x)+800(x﹣3)=15800
解得:x=5
∴17﹣x=12,18﹣x=13,x﹣3=2
答:当运送总费用为15800元时,从A地运往甲地5台,运往乙地12台;从B地运往甲地13台,运往乙地2台.
(3)有运送方案比(2)中方案的总运费低.
设总运费为y元,得:
y=600x+500(17﹣x)+400(18﹣x)+800(x﹣3)=500x+13300
y随x增大而增大
又∵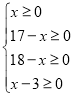 得:3≤x≤17
得:3≤x≤17
∴当x=3时,y有最小值,为y=500×3+13300=14800
∴方案为:从A地运往甲地3台,运往乙地14台;从B地运往甲地15台,运往乙地0台.最低运费为14800元.


科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
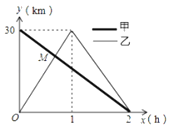
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
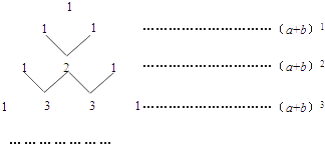
(1)根据上面的规律,则(a+b)5的展开式=________.
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
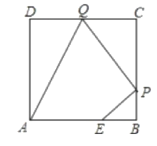
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟![]() h到达B地;
h到达B地;
(4)乙车行驶![]() 小时或
小时或![]() 小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,排列成如图所示的数表:
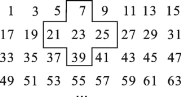
(1)十字框中的五个数的和与中间数23有什么关系?
(2)设中间数为![]() ,用式子表示十字框中五个数之和.
,用式子表示十字框中五个数之和.
(3)将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
(4)十字框中的五个数之和能等于2015吗?若能,请写出这五个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com