
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() ±μ ΨΡ≥…Χ≥Γ“ΜΧλΒΡ ÷ΧαΒγΡ‘œζ έΕν”κœζ έΝΩΒΡΙΊœΒΘ§
±μ ΨΡ≥…Χ≥Γ“ΜΧλΒΡ ÷ΧαΒγΡ‘œζ έΕν”κœζ έΝΩΒΡΙΊœΒΘ§![]() ±μ ΨΗΟ…Χ≥Γ“ΜΧλΒΡ ÷ΧαΒγΡ‘œζ έ≥…±Ψ”κœζ έΝΩΒΡΙΊœΒΘ°
±μ ΨΗΟ…Χ≥Γ“ΜΧλΒΡ ÷ΧαΒγΡ‘œζ έ≥…±Ψ”κœζ έΝΩΒΡΙΊœΒΘ°
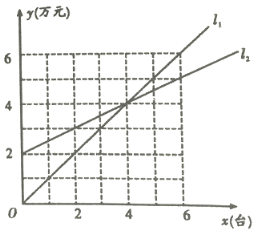
Θ®1Θ©Β±œζ έΝΩ![]() Χ® ±Θ§œζ έΕν
Χ® ±Θ§œζ έΕν![]() _______________Άρ‘ΣΘ§œζ έ≥…±Ψ
_______________Άρ‘ΣΘ§œζ έ≥…±Ψ![]() ___________Άρ‘ΣΘ§άϊ»σΘ®œζ έΕν
___________Άρ‘ΣΘ§άϊ»σΘ®œζ έΕν![]() œζ έ≥…±ΨΘ©
œζ έ≥…±ΨΘ©![]() _____________Άρ‘ΣΘ°
_____________Άρ‘ΣΘ°
Θ®2Θ©“ΜΧλœζ έ__________Χ® ±Θ§œζ έΕνΒ»”Ύœζ έ≥…±ΨΘ°
Θ®3Θ©Β±œζ έΝΩ________ ±Θ§ΗΟ…Χ≥Γ”·άϊΘ® ’»κ¥σ”Ύ≥…±ΨΘ©Θ§Β±œζ έΝΩ__________ ±Θ§ΗΟ…Χ≥ΓΩςΥπΘ® ’»κ–Γ”Ύ≥…±ΨΘ©Θ°
Θ®4Θ©![]() Ε‘”ΠΒΡΚ· ΐΙΊœΒ Ϋ «______________Θ°
Ε‘”ΠΒΡΚ· ΐΙΊœΒ Ϋ «______________Θ°
Θ®5Θ©«κΡψ–¥≥ωάϊ»σ![]() Θ®Άρ‘ΣΘ©”κœζ έΝΩ
Θ®Άρ‘ΣΘ©”κœζ έΝΩ![]() Θ®Χ®Θ©ΦδΒΡΚ· ΐΙΊœΒ Ϋ_____________Θ§Τδ÷–Θ§
Θ®Χ®Θ©ΦδΒΡΚ· ΐΙΊœΒ Ϋ_____________Θ§Τδ÷–Θ§![]() ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
ΒΡ»Γ÷ΒΖΕΈß «__________Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©2Θ§3Θ§Θ≠1ΘΜΘ®2Θ©4ΘΜ Θ®3Θ©¥σ”Ύ4Χ®Θ§–Γ”Ύ4Χ®ΘΜΘ®4Θ©y=xΘΜΘ®5Θ©Q=![]() Θ§xΓί0«“xΈΣ’ϊ ΐΘ°
Θ§xΓί0«“xΈΣ’ϊ ΐΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®2Θ©ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Ω…ΒΟΘΚ
Θ§Ω…ΒΟΘΚ![]() Θ§
Θ§![]() ΒΡΫΜΒψΉχ±ξ «ΘΚ(4Θ§4)Θ§ΫχΕχΦ¥Ω…«σΫβΘΜ
ΒΡΫΜΒψΉχ±ξ «ΘΚ(4Θ§4)Θ§ΫχΕχΦ¥Ω…«σΫβΘΜ
Θ®3Θ©÷±Ϋ”ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®4Θ©…η![]() ΒΡΫβΈω ΫΈΣΘΚy=kxΘ§ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
ΒΡΫβΈω ΫΈΣΘΚy=kxΘ§ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§Φ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®5Θ©…η![]() ΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§ΫχΕχΦ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
ΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§ΗυΨί¥ΐΕ®œΒ ΐΖ®Θ§ΫχΕχΦ¥Ω…ΒΟΒΫ¥πΑΗΘΜ
Θ®1Θ©ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Ω…ΒΟΘΚΒ±œζ έΝΩ
Θ§Ω…ΒΟΘΚΒ±œζ έΝΩ![]() Θ®Χ®Θ© ±Θ§œζ έΕν
Θ®Χ®Θ© ±Θ§œζ έΕν![]() 2Θ®Άρ‘ΣΘ©Θ§œζ έ≥…±Ψ
2Θ®Άρ‘ΣΘ©Θ§œζ έ≥…±Ψ![]() 3Θ®Άρ‘ΣΘ©Θ§άϊ»σΘ®œζ έΕν
3Θ®Άρ‘ΣΘ©Θ§άϊ»σΘ®œζ έΕν![]() œζ έ≥…±ΨΘ©
œζ έ≥…±ΨΘ©![]() -1Θ®Άρ‘ΣΘ©Θ°
-1Θ®Άρ‘ΣΘ©Θ°
Ι ¥πΑΗ «ΘΚ2Θ§3Θ§Θ≠1ΘΜ
Θ®2Θ©ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Ω…ΒΟΘΚ
Θ§Ω…ΒΟΘΚ![]() Θ§
Θ§![]() ΒΡΫΜΒψΉχ±ξ «ΘΚ(4Θ§4)Θ§
ΒΡΫΜΒψΉχ±ξ «ΘΚ(4Θ§4)Θ§
Γύ“ΜΧλœζ έ4Χ® ±Θ§œζ έΕνΒ»”Ύœζ έ≥…±ΨΘ°
Ι ¥πΑΗ «ΘΚ4ΘΜ
Θ®3Θ©ΗυΨίΆΦœσ![]() Θ§
Θ§![]() Θ§Ω…ΒΟΘΚΒ±œζ έΝΩ¥σ”Ύ4Χ® ±Θ§ΗΟ…Χ≥Γ”·άϊΘ® ’»κ¥σ”Ύ≥…±ΨΘ©Θ§Β±œζ έΝΩ–Γ”Ύ4Χ® ±Θ§ΗΟ…Χ≥ΓΩςΥπΘ® ’»κ–Γ”Ύ≥…±ΨΘ©Θ°
Θ§Ω…ΒΟΘΚΒ±œζ έΝΩ¥σ”Ύ4Χ® ±Θ§ΗΟ…Χ≥Γ”·άϊΘ® ’»κ¥σ”Ύ≥…±ΨΘ©Θ§Β±œζ έΝΩ–Γ”Ύ4Χ® ±Θ§ΗΟ…Χ≥ΓΩςΥπΘ® ’»κ–Γ”Ύ≥…±ΨΘ©Θ°
Ι ¥πΑΗ «ΘΚ¥σ”Ύ4Χ®Θ§–Γ”Ύ4Χ®ΘΜ
Θ®4Θ©…η![]() ΒΡΫβΈω ΫΈΣΘΚy=kxΘ§
ΒΡΫβΈω ΫΈΣΘΚy=kxΘ§
Α―(4Θ§4)¥ζ»κy=kxΒΟΘΚ4=4kΘ§ΫβΒΟΘΚk=1Θ§
Γύ![]() ΒΡΫβΈω ΫΈΣΘΚy=xΘ§
ΒΡΫβΈω ΫΈΣΘΚy=xΘ§
Ι ¥πΑΗ «ΘΚy=xΘΜ
Θ®5Θ©…η![]() ΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
ΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§
Α―(0Θ§2)Θ§(4Θ§4)¥ζ»κy=kx+bΘ§ΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ![]() ΒΡΫβΈω ΫΈΣΘΚy=
ΒΡΫβΈω ΫΈΣΘΚy=![]() x+2Θ§
x+2Θ§
ΓύQ=![]() Θ§
Θ§
![]() ΒΡ»Γ÷ΒΖΕΈß «ΘΚxΓί0«“xΈΣ’ϊ ΐΘ°
ΒΡ»Γ÷ΒΖΕΈß «ΘΚxΓί0«“xΈΣ’ϊ ΐΘ°
Ι ¥πΑΗ «ΘΚQ=![]() Θ§xΓί0«“xΈΣ’ϊ ΐΘ°
Θ§xΓί0«“xΈΣ’ϊ ΐΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®8Ζ÷Θ©»γΆΦΥυ ΨΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§AB=2![]() Θ§BC=2Θ§CD=1Θ§AD=5Θ§«“ΓœC=90ΓψΘ§«σΥΡ±Ώ–ΈABCDΒΡΟφΜΐ.
Θ§BC=2Θ§CD=1Θ§AD=5Θ§«“ΓœC=90ΓψΘ§«σΥΡ±Ώ–ΈABCDΒΡΟφΜΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®3Ζ÷Θ©“‘œ¬ΥΡ÷÷―ΊAB’έΒΰΒΡΖΫΖ®÷–Θ§≤Μ“ΜΕ®Ρή≈–Ε®÷Ϋ¥χΝΫΧθ±ΏœΏaΘ§bΜΞœύΤΫ––ΒΡ «Θ® Θ©

A. »γΆΦ1Θ§’ΙΩΣΚσ≤βΒΟΓœ1=Γœ2
B. »γΆΦ2Θ§’ΙΩΣΚσ≤βΒΟΓœ1=Γœ2«“Γœ3=Γœ4
C. »γΆΦ3Θ§≤βΒΟΓœ1=Γœ2
D. »γΆΦ4Θ§’ΙΩΣΚσ‘Ό―ΊCD’έΒΰΘ§ΝΫΧθ’έΚέΒΡΫΜΒψΈΣOΘ§≤βΒΟOA=OBΘ§OC=OD
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœφΈςΉ‘÷Έ÷ίΖγΨΑ”≈ΟάΘ§Έο≤ζΖαΗΜΘ§“ΜΆβΒΊ”ΈΩΆΒΫΡ≥ΧΊ≤ζΉ®”ΣΒξΘ§ΉΦ±ΗΙΚ¬ρΨΪΦ”ΙΛΒΡΕΙΗ·»ιΚΆβ®ΚοΧ“Ιϊ÷≠ΝΫ÷÷Κ–ΉΑΧΊ≤ζΘ°»τΙΚ¬ρ3Κ–ΕΙΗ·»ιΚΆ2Κ–β®ΚοΧ“Ιϊ÷≠Ι≤–η180‘ΣΘΜΙΚ¬ρ1Κ–ΕΙΗ·»ιΚΆ3Κ–β®ΚοΧ“Ιϊ÷≠Ι≤–η165‘ΣΘ°
Θ®1Θ©«κΖ÷±π«σ≥ωΟΩΚ–ΕΙΗ·»ιΚΆΟΩΚ–β®ΚοΧ“Ιϊ÷≠ΒΡΦέΗώΘΜ
Θ®2Θ©ΗΟ”ΈΩΆΙΚ¬ρΝΥ4Κ–ΕΙΗ·»ιΚΆ2Κ–β®ΚοΧ“Ιϊ÷≠Θ§Ι≤–ηΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
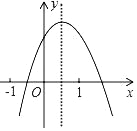
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐy=ax2+bx+cΒΡΆΦœσ»γΆΦ ΨΘ§œ¬Ν–Ϋα¬έΘΚ
Θ®1Θ©bΘΦ0ΘΜΘ®2Θ©cΘΨ0ΘΜΘ®3Θ©b2©¹4acΘΨ0ΘΜ Θ®4Θ©a©¹b+cΘΦ0Θ§
Θ®5Θ©2a+bΘΦ0ΘΜ Θ®6Θ©abcΘΨ0ΘΜΤδ÷–’ΐ»ΖΒΡ «_____ΘΜΘ®Χν–¥–ρΚ≈Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bxΘ®aΓΌ0Θ©ΙΐΒψEΘ®10Θ§0Θ©Θ§ΨΊ–ΈABCDΒΡ±ΏAB‘ΎœΏΕΈOE…œΘ®ΒψA‘ΎΒψBΒΡΉσ±ΏΘ©Θ§ΒψCΘ§D‘Ύ≈ΉΈοœΏ…œΘ°…ηAΘ®tΘ§0Θ©Θ§Β±t=2 ±Θ§AD=4Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘ°
Θ®2Θ©Β±tΈΣΚΈ÷Β ±Θ§ΨΊ–ΈABCDΒΡ÷ή≥Λ”–Ήν¥σ÷ΒΘΩΉν¥σ÷Β «Εύ…ΌΘΩ
Θ®3Θ©±Θ≥÷t=2 ±ΒΡΨΊ–ΈABCD≤ΜΕ·Θ§œρ”“ΤΫ“Τ≈ΉΈοœΏΘ°Β±ΤΫ“ΤΚσΒΡ≈ΉΈοœΏ”κΨΊ–ΈΒΡ±Ώ”–ΝΫΗωΫΜΒψGΘ§HΘ§«“÷±œΏGHΤΫΖ÷ΨΊ–ΈΒΡΟφΜΐ ±Θ§«σ≈ΉΈοœΏΤΫ“ΤΒΡΨύάκΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥ°ΝζΆΖΙΊ±’≤ΜΫτΜα‘λ≥…ΒΈΥ°Θ§–ΓΟς”ΟΩ…“‘œ‘ ΨΥ°ΝΩΒΡ»ίΤςΉωΆΦΔΌΥυ ΨΒΡ ‘―ιΘ§≤ΔΗυΨί ‘―ι ΐΨίΜφ÷Τ≥ωΆΦΔΎΥυ ΨΒΡ»ίΤςΡΎ ΔΥ°ΝΩWΘ®LΘ©”κΒΈΥ° ±ΦδtΘ®hΘ©ΒΡΚ· ΐΙΊœΒΆΦœσΘ§«κΫαΚœΆΦœσΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©»ίΤςΡΎ‘≠”–Υ°Εύ…ΌΘΩ
Θ®2Θ©«σW”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΦΤΥψ‘Ύ’β÷÷ΒΈΥ°Ή¥Χ§œ¬“ΜΧλΒΡΒΈΥ°ΝΩ «Εύ…Ό…ΐΘΩ

ΆΦ ΔΌ ΆΦΔΎ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ¬δ ΒΒ≥÷–―κΓΑ≥ΛΫ≠¥σ±ΘΜΛΓ±–¬ΖΔ’ΙάμΡνΘ§Έ“ –≥÷–χΆΤΫχ≥ΛΫ≠ΑΕœΏ±ΘΜΛΘ§ΜΙΕ¥ΆΞΚΰΚΆ≥ΛΫ≠Υ°«εΑΕ¬ΧΒΡΉ‘»Μ…ζΧ§‘≠Ο≤Θ°Ρ≥ΙΛ≥ΧΕ”ΗΚ‘πΕ‘“ΜΟφΜΐΈΣ33000ΤΫΖΫΟΉΒΡΖ«Ζ®…Α ·¬κΆΖΫχ––≤π≥ΐΘ§ΜΊΧνΆΝΖΫΚΆΗ¥¬Χ ©ΙΛΘ§ΈΣΝΥΥθΕΧΙΛΤΎΘ§ΗΟΙΛ≥ΧΕ”‘ωΦ”ΝΥ»ΥΝΠΚΆ…η±ΗΘ§ ΒΦ ΙΛΉς–߬ ±»‘≠ΦΤΜ°ΟΩΧλΧαΗΏΝΥ20%Θ§ΫαΙϊΧα«Α11ΧλΆξ≥…»ΈΈώΘ§«σ ΒΦ ΤΫΨυΟΩΧλ ©ΙΛΕύ…ΌΤΫΖΫΟΉΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§“‘Βψ
Θ§“‘Βψ![]() ΈΣ‘≤–ΡΘ§8ΈΣΑκΨΕΒΡ‘≤”κ
ΈΣ‘≤–ΡΘ§8ΈΣΑκΨΕΒΡ‘≤”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§Ιΐ
ΝΫΒψΘ§Ιΐ![]() Ής÷±œΏ
Ής÷±œΏ![]() ”κ
”κ![]() ÷αΗΚΖΫœρœύΫΜ≥…
÷αΗΚΖΫœρœύΫΜ≥…![]() ΒΡΫ«Θ§«“ΫΜ
ΒΡΫ«Θ§«“ΫΜ![]() ÷α”Ύ
÷α”Ύ![]() ΒψΘ§“‘Βψ
ΒψΘ§“‘Βψ![]() ΈΣ‘≤–ΡΒΡ‘≤”κ
ΈΣ‘≤–ΡΒΡ‘≤”κ![]() ÷αœύ«–”ΎΒψ
÷αœύ«–”ΎΒψ![]() .
.

Θ®1Θ©«σ÷±œΏ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫΪ![]() “‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»―Ί
“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»―Ί![]() ÷αœρΉσΤΫ“ΤΘ§Β±
÷αœρΉσΤΫ“ΤΘ§Β±![]() ΒΎ“Μ¥Έ”κ
ΒΎ“Μ¥Έ”κ![]() Άβ«– ±Θ§«σ
Άβ«– ±Θ§«σ![]() ΤΫ“ΤΒΡ ±Φδ.
ΤΫ“ΤΒΡ ±Φδ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com