
���� ��1���ɶ�����ϵ����Ϊ0���Ҹ����б�ʽ����0�����m�ķ�Χ���ɣ�
��2����Ϊx=1������������ֻ��$\frac{2m-2}{m}$���������������m��ֵ���ó������ߵĽ���ʽΪy=x2-x������ƽ�Ƶ����ʼ��ɵó�����Ľ���ʽy=��x-2��2-��x-2����
��3�������������x�ᡢy�ύ�����֪꣬ͼ��G���Ա���ȡֵ��Χ����a+b��x�ĺ�����ϵ����ͼ��G���Ա���ȡֵ��Χ��ȷ�����ֵ����Сֵ��
��� �⣺��1���߹���x��һԪ���η���mx2-��3m-2��x+2m-2=0����������ȵ�ʵ������
��m��0�ҡ�=��3m-2��2-4m��2m-2��=��m-2��2��0��
��m�ķ�ΧΪm��0��m��2��
��2����x=1��������
��ֻ��$\frac{2m-2}{m}$=2-$\frac{2}{m}$��������
��m������������m��0��m��2��
��m=1��
��m=1ʱ�������ߵĽ���ʽΪy=x2-x��
������ͼ������ƽ��2����λ���ȣ���y=��x-2��2-��x-2����
��y=x2-5x+6��
��3��y=x2-5x+6��x��Ľ�������Ϊ��2��0������3��0������y��Ľ�������Ϊ��0��6����
��A��0��6����B��3��0��
��������C��x�����������п��Ҳ�ĵ�ΪB����y�ύ�����A������������A��B֮��IJ���Ϊͼ��G������A��B���㣩��
��ͼ��G���Ա���ȡֵ��ΧΪ��0��x��3��
�ߵ�P��a��b��ΪG��һ���㣬
��a+b=x+x2-5x+6=x2-4x+6=��x-2��2+2��
��x=2ʱ��a+b����СֵΪ2��
��x=0ʱ��a+b�����ֵΪ6��
��a+b��ȡֵ��ΧΪ��2��a+b��6��
���� ������Ҫ������ô���ϵ��������κ����Ľ���ʽ�����κ�����x��Ľ��㣬����ϵ���Ĺ�ϵ��ƽ�Ƶ����ʵ�֪ʶ�����������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
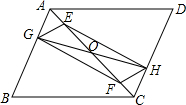 ��ͼ��ʾ����֪����?ABCD�У���E��F��AC�ϣ���AF=CE����G��H�ֱ���AB��CD�ϣ���AG=CH��AC��GH�ཻ�ڵ�O����֤���ı���EGFH��ƽ���ı��Σ�
��ͼ��ʾ����֪����?ABCD�У���E��F��AC�ϣ���AF=CE����G��H�ֱ���AB��CD�ϣ���AG=CH��AC��GH�ཻ�ڵ�O����֤���ı���EGFH��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
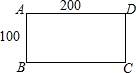 ��ͳ�����ϣ��ס�������ũ����ĵ�λ��������ı���1��2����Ҫ��һ�鳤Ϊ200m����100m�ij��������ط�Ϊ�����֣��ֱ���ֲ���������ʹ�ס�������������ܲ����ı���3��10
��ͳ�����ϣ��ס�������ũ����ĵ�λ��������ı���1��2����Ҫ��һ�鳤Ϊ200m����100m�ij��������ط�Ϊ�����֣��ֱ���ֲ���������ʹ�ס�������������ܲ����ı���3��10�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
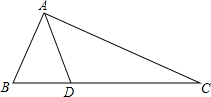 ��ͼ����ABC�У�AD�ǽ�ƽ���ߣ���AC=AB+BD����C=26�㣬�����B�Ķ�����
��ͼ����ABC�У�AD�ǽ�ƽ���ߣ���AC=AB+BD����C=26�㣬�����B�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
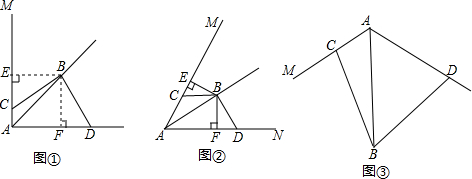
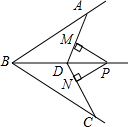 ��ͼ��BD�ǡ�ABC��ƽ���ߣ�AB=BC����P��BD�ϣ�PM��AD��PN��CD��M��N�ֱ��Ǵ��㣬��֤��PM=PN��
��ͼ��BD�ǡ�ABC��ƽ���ߣ�AB=BC����P��BD�ϣ�PM��AD��PN��CD��M��N�ֱ��Ǵ��㣬��֤��PM=PN���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com