
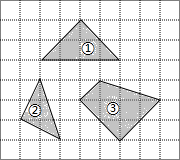
 如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③.
如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③. 分析 利用相似三角形的判定和性质分别求出各多边形竖直部分线段长度之和与水平部分线段长度之和,再比较即可.
解答 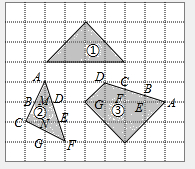 解:假设每个小正方形的边长为1,
解:假设每个小正方形的边长为1,
①m=1+2+1=4,n=2+4=6,
则m≠n;
②在△ACN中,BM∥CN,
∴$\frac{BM}{CN}$=$\frac{1}{2}$,
∴BM=$\frac{1}{2}$,
在△AGF中,DM∥NE∥FG,
∴$\frac{AM}{AG}$=$\frac{1}{3}$,$\frac{AN}{AG}$=$\frac{2}{3}$,
得DM=$\frac{1}{3}$,NE=$\frac{2}{3}$,
∴m=2+$\frac{1}{2}$=2.5,n=$\frac{1}{2}$+1+$\frac{1}{3}$+$\frac{2}{3}$=2.5,
∴m=n;
③由②得:BE=$\frac{1}{3}$,CF=$\frac{2}{3}$,
∴m=2+2+$\frac{2}{3}$+1+$\frac{1}{3}$=6,n=4+2=6,
∴m=n,
则这三个多边形中满足m=n的是②和③.
故答案为:②③.
点评 本题考查了相似多边形的判定和性质,对于有中点的三角形可以利用三角形中位线定理得出;本题线段比较多要依次相加,做到不重不漏.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
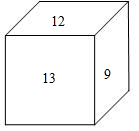 如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为69.
如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为69.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | 1 | 1.1 | 1.2 | 1.3 |
| x2+12x-15 | -2 | -0.59 | 0.84 | 2.29 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第17个数 | B. | 第18个数 | C. | 第19个数 | D. | 第20个数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com