
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元.
(2)商场计划购进甲、乙两种玩具共80件,商场决定此次进货的总资金不超过1500元,那么甲种玩具最少购进多少个?
【答案】(1)15元/件;25元/件 (2)50个
【解析】
(1)设甲种玩具进价x元/件,则乙种玩具进价为(40-x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具y件,则购进乙种玩具(80-y)件,根据商场决定此次进货的总资金不超过1500元,可列出不等式求解.
解:(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,根据题意可得:
![]()
解得:x=15,
经检验x=15是原方程的解.
故40﹣x=25
答:甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(80﹣y)件,
15y+25(80﹣y)≤1500
解得:y≥50
答:甲种玩具最少购进50个.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是弧AB的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交D的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交D的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;
(2)当OB=2时,求AH的长
查看答案和解析>>
科目:初中数学 来源: 题型:
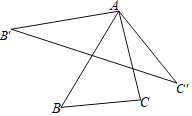
【题目】如图,将![]() 的边
的边![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,边AC绕着点A逆时针旋转
,边AC绕着点A逆时针旋转![]() 得到
得到![]() ,联结
,联结![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“双旋三角形”.如果等边
的“双旋三角形”.如果等边![]() 的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
的边长为a,那么它的“双旋三角形”的面积是__________(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有值的全体叫做闭区间、表示为
的所有值的全体叫做闭区间、表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式;
上的“闭函数”,求此一次函数的解析式;
(3)若实数![]() 满足
满足![]() .且
.且![]() ,当二次函数
,当二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”时,求
上的“闭函数”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
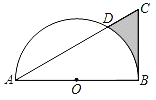
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4![]() ,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“和谐号”列车缓缓停靠在梅州西站,我市正式进入了高铁时代.与普通列车相比,“和谐号”列车时速更快,安全性更好.已知“梅州西—广州南”全程大约![]() 千米,“和谐号”
千米,“和谐号”![]() 次列车平均每小时比普通列车多行驶
次列车平均每小时比普通列车多行驶![]() 千米,其行驶时间是普通列车行驶时间的
千米,其行驶时间是普通列车行驶时间的![]() (两列车中途停留时间均除外).
(两列车中途停留时间均除外).
(1)经查询,“和谐号”![]() 次列车从梅州西到广州南,中途合计停站时间为
次列车从梅州西到广州南,中途合计停站时间为![]() 分钟,求乘坐“和谐号”
分钟,求乘坐“和谐号”![]() 次列车从梅州西到广州南需要多长时间;
次列车从梅州西到广州南需要多长时间;
(2)据了解,梅州西站后期还会引进更快的“复兴号”高铁,届时跑完![]() 千米的路程最多只需要
千米的路程最多只需要![]() 小时,请问“复兴号”高铁的速度每小时至少比“和谐号”列车快了多少千米.
小时,请问“复兴号”高铁的速度每小时至少比“和谐号”列车快了多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快复工复产,某企业需运输批物资.据调查得知,2辆大货车与3辆小货车一次可以运输600箱;5辆大货车与6辆小货车一次可以运输1350箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资;
(2)计划用两种货车共12辆运输这批物资,每辆大货车一次需费用5 000元,每辆小货车一次需费用3000元.若运输物资不少于1500箱,且总费用小于54000元,请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
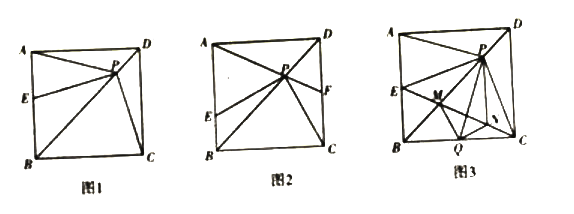
【题目】如图1,在正方形ABCD中,AD=6,点P是对角线BD上任意一点,连接PA,PC,过点P作PE⊥PC交直线AB于点E.
(1)求证: PC=PE;
(2)延长AP交直线CD于点F.
①如图2,若点F是CD的中点,求△APE的面积;
②若△APE的面积是![]() ,则DF的长为_________;
,则DF的长为_________;
(3)如图3,点E在边AB上,连接EC交BD于点M,作点E关于BD的对称点Q,连接PQ, MQ,过点P作![]() 交EC于点N,连接
交EC于点N,连接![]() ,若
,若![]() ,则
,则![]() 的面积是________.
的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com