
【题目】如图,在平面直角坐标系xOy中,ABCO的顶点A,B的坐标分别是A(3,0),B(0,2),动点P在直线y=![]() x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.
x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.

【答案】(0,0)或(![]() ,1)或(3﹣
,1)或(3﹣![]() ,
,![]() ).
).
【解析】分析:设P(x,![]() ),⊙P的半径为r,由题意BC⊥y轴,直线OP的解析式y=
),⊙P的半径为r,由题意BC⊥y轴,直线OP的解析式y=![]() ,直线OC的解析式为
,直线OC的解析式为![]() 可知OP⊥OC,分分四种情形讨论即可得出答案.
可知OP⊥OC,分分四种情形讨论即可得出答案.
详解:①当⊙P与BC相切时,∵动点P在直线y=![]() x上,
x上,
∴P与O重合,此时圆心P到BC的距离为OB, ∴P(0,0).
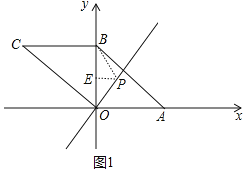
②如图1中,当⊙P与OC相切时,则OP=BP,△OPB是等腰三角形,作PE⊥y轴于E,则EB=EO,易知P的纵坐标为1,可得P(![]() ,1).
,1).
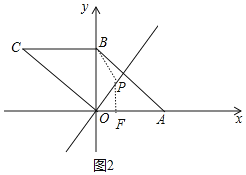
③如图2中,当⊙P与OA相切时,则点P到点B的距离与点P到x轴的距离线段,可得:![]() ,解得x=3+
,解得x=3+![]() 或3-
或3-![]() , ∵x=3+
, ∵x=3+![]() >OA,∴P不会与OA相切,
>OA,∴P不会与OA相切,
∴x=3+![]() 不合题意, ∴p(3-
不合题意, ∴p(3-![]() ,
,![]() ).
).
④如图3中,当⊙P与AB相切时,设线段AB与直线OP的交点为G,此时PB=PG,
∵OP⊥AB,∴∠BGP=∠PBG=90°不成立,∴此种情形,不存在P.

综上所述,满足条件的P的坐标为(0,0)或(![]() ,1)或(3-
,1)或(3-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般来说,依据数学研究对象本质属性的相同点和差异点,将数学对象分为不同种类的数学思想叫做“分类”的思想;将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法.请依据分类的思想和分类讨论的方法解决下列问题:
如图,在![]() 中,
中,![]() .
.

![]() 若
若![]() 是锐角,请探索在直线
是锐角,请探索在直线![]() 上有多少个点
上有多少个点![]() ,能保证
,能保证![]() (不包括全等)?
(不包括全等)?
![]() 请对
请对![]() 进行恰当的分类,直接写出每一类在直线
进行恰当的分类,直接写出每一类在直线![]() 上能保证
上能保证![]() (不包括全等)的点
(不包括全等)的点![]() 的个数?
的个数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等边三角形ABC的边长为4,两顶点B、C分别在y轴的正半轴和x轴的正半轴上运动,显然,当OA⊥BC于点D时,顶点A到原点O的距离最大,试求出此时线段OA的长.
(2)如图2,在Rt△ACB中,∠ACB=90°,AC=3,BC=4,两顶点B、C分别在x轴的正半制和y轴的正半轴上运动,求出顶点A到原点O的最大距离.
(3)如图3,正六边形ABCDEF的边长为4,顶点B、C分别在x轴正半轴和y轴正半轴上运动,直接写出顶点E到原点O的距离的最大值和最小值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 在直角坐标平面内,三个顶点的坐标分别为
在直角坐标平面内,三个顶点的坐标分别为![]() 、
、![]() 、
、![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).

![]() 向下平移
向下平移![]() 个单位长度得到的
个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
![]() 以点
以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;(画出图形)
的坐标是________;(画出图形)
![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小华像这样解分式方程![]()
解:移项,得:![]()
通分,得:![]()
整理,得:![]() 分子值取0,得:x+5=0
分子值取0,得:x+5=0
即:x=﹣5
经检验:x=﹣5是原分式方程的解.
(1)小华这种解分式方程的新方法,主要依据是 ;
(2)试用小华的方法解分式方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com