
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.

【答案】![]()
【解析】
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,根据折叠的性质得到DE⊥CF,OC=OF,再根据等角的余角相等得∠1=∠EDC,而∠EDC=∠A,则∠1=∠A,所以FC=FA,同理可得FC=FB,于是有CF=![]() AB,OC=
AB,OC=![]() AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=
AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=![]() ,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=
,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=![]() ,OD=
,OD=![]() ,再计算OE+OD即可.
,再计算OE+OD即可.
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,如图,

∴DE⊥CF,OC=OF,
∵∠EDC+∠OCD=90°,∠1+∠OCD=90°,
∴∠1=∠EDC,
而∠EDC=∠A,
∴∠1=∠A,
∴FC=FA,
同理可得FC=FB,
∴CF=![]() AB,
AB,
∴OC=![]() AB,
AB,
在Rt△ABC中,∠C=90°,AC=3,
∴tanA=![]() ,
,
∴BC=4,
∴AB=![]() =5,
=5,
∴OC=![]() ,
,
在Rt△OEC中,tan∠1=tan∠A=![]() ,
,
∴OE=![]() ,
,
在Rt△ODC中,tan∠ODC=tan∠A=![]() ,
,
∴OD=![]() ,
,
∴DE=OD+OE=![]() +
+![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的有(____)
①DC′平分∠BDE;②BC长为![]() ;③△
;③△![]() 是等腰三角形;④△CED的周长等于BC的长.
是等腰三角形;④△CED的周长等于BC的长.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,一次函数的图象与抛物线交于
三点,一次函数的图象与抛物线交于![]() ,
,![]() 两点.
两点.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 当两函数的函数值都随着
当两函数的函数值都随着![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
![]() 当自变量
当自变量![]() 满足什么范围时,一次函数值大于二次函数值.
满足什么范围时,一次函数值大于二次函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
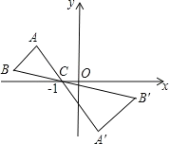
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列各题:
(1)先化简,再求代数式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是锐角,且sin(α+15°)=![]() .计算
.计算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,ABCO的顶点A,B的坐标分别是A(3,0),B(0,2),动点P在直线y=![]() x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.
x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com