
����Ŀ����1����ͼ1���ȱ�������ABC�ı߳�Ϊ4��������B��C�ֱ���y����������x������������˶�����Ȼ����OA��BC�ڵ�Dʱ������A��ԭ��O�ľ�������������ʱ�߶�OA�ij���
��2����ͼ2����Rt��ACB�У���ACB=90�㣬AC=3��BC=4��������B��C�ֱ���x��������ƺ�y������������˶����������A��ԭ��O�������룮
��3����ͼ3����������ABCDEF�ı߳�Ϊ4������B��C�ֱ���x���������y�����������˶���ֱ��д������E��ԭ��O�ľ�������ֵ����Сֵ��



���𰸡���1��OA=2+2![]() ����2��2+
����2��2+![]() ����3��2+
����3��2+![]() ��4
��4![]() .
.
��������
��1����ֱ�����������AD��OD���ɣ�
��2����ͼ2�У�ȡBC���е�K������OK��AK��OA����ΪOA��AK��OK���Ƴ�O��K��A����ʱ��OA��ֵ���
��3����ͼ3�У�ȡBC���е�K������OK��EK��OE����ΪOE��OK��EK���Ƴ�O��K��E����ʱ��OE��ֵ�����C��O�غ�ʱ��OE��ֵ��С.
��1����ͼ1�У�

�ߡ�ABC�ǵȱ������Σ�
��AB=BC=AC=4����ACD=60�㣬
��AD��BC��
��BD=CD��AD=ACsin60��=2![]() ��
��
��OD=![]() BC=2��
BC=2��
��OA=2+2![]() ��
��
��2����ͼ2�У�ȡBC���е�K������OK��AK��OA��
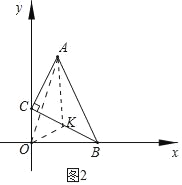
��Rt��BOC��OK=![]() BC=2��
BC=2��
��Rt��ACK��AK=![]() =
=![]() ��
��
��OA��AK+OK��
��O��K��A����ʱ��OA��ֵ������ֵΪ2+![]() ��
��
��3����ͼ3�У�ȡBC���е�K������OK��EK��OE��

��OK=![]() BC=2��EC=4
BC=2��EC=4![]() ����ECK=90�㣬
����ECK=90�㣬
��Rt��ECK��EK=![]() =2
=2![]() ��
��
��OE��OK+EK��
��O��K��E����ʱ��OE��ֵ������ֵΪ2+2![]() ��
��
����C��O�غ�ʱ��OE��ֵ��С����СֵΪ4![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ������������ֱ���
��ͼ������������ֱ���![]() ��
��![]() ��
��![]() ���㣬һ�κ�����ͼ���������߽���
���㣬һ�κ�����ͼ���������߽���![]() ��
��![]() ���㣮
���㣮

![]() ���
���![]() ��
��![]() ��
��![]() �����ꣻ
�����ꣻ
![]() ���������ĺ���ֵ������
���������ĺ���ֵ������![]() �������������
�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ���Ա���
���Ա���![]() ����ʲô��Χʱ��һ�κ���ֵ���ڶ��κ���ֵ��
����ʲô��Χʱ��һ�κ���ֵ���ڶ��κ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С���û������εİ취��������һ��ͼ�������ܰ����ɼ�������ȥ��������������Щ����ͼ�Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�A��0��3����B��4��0����C����1����1������ P �߶� AB��һ���������߶� AB ��ԭ�� O ��תһ������ P �Ķ�Ӧ��Ϊ P�䣬�� P��C �����ֵΪ_____����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�DΪBC���ϵ�һ�㣬����B=36�㣬AB=AC=BD=2��
��1����CD�ij���
��2�����ô�ͼ��sin18����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90��,��ACΪб������������ֱ��������COA����֪BC=8,OB=10![]() ,����һֱ�DZ�AB�ij�Ϊ__________.
,����һֱ�DZ�AB�ij�Ϊ__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ABCO�Ķ���A��B������ֱ���A��3��0����B��0��2��������P��ֱ��y=![]() x���˶����Ե�PΪԲ�ģ�PB��Ϊ�뾶�ġ�P���P�˶�������P���ı���ABCO�ı�����ֱ������ʱ��P�������Ϊ_____��
x���˶����Ե�PΪԲ�ģ�PB��Ϊ�뾶�ġ�P���P�˶�������P���ı���ABCO�ı�����ֱ������ʱ��P�������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
| �� |
| 0 | 1 | 3 | �� |
| �� |
| 1 | 3 | 1 | �� |
�������ж�����ȷ���ǣ� ��
A. �����߿������� B. ��������![]() �ύ�ڸ�����
�ύ�ڸ�����
C. ��![]() ʱ��
ʱ��![]() D. ����
D. ����![]() ��������3��4֮��
��������3��4֮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c�����㣨��1��0�����Գ���l��ͼ��ʾ�������н��ۣ���abc��0����a��b+c=0����2a+c��0����a+b��0������������ȷ�Ľ����ǣ� ��

A���٢� B���ڢ� C���ڢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com