
分析 将y1=2,y1=2,代入原方程组可以得到x与n的关系,然后代入$\frac{y_1}{x_1}+\frac{{2{y_2}}}{x_2}=\frac{4}{n}$,可以求得y2的值,再将方程组$\left\{\begin{array}{l}x=n(y+2)\\{x^2}+4{y^2}=4t\end{array}\right.$中的x消去即可得到关于y的一元二次方程,然后根据韦达定理即可求得n和t的值.
解答 解:∵y1=2,
∴$\left\{\begin{array}{l}{{x}_{1}=4n}\\{{{x}_{1}}^{2}+4{{y}_{1}}^{2}=4t}\end{array}\right.$,
将x1=4n,y1=2代入$\frac{y_1}{x_1}+\frac{{2{y_2}}}{x_2}=\frac{4}{n}$,得
$\frac{2}{4n}+\frac{2{y}_{2}}{n({y}_{2}+2)}=\frac{4}{n}$
化简,得
$\frac{1}{2}+\frac{2{y}_{2}}{{y}_{2}+2}=4$,
解得${y}_{2}=-\frac{14}{3}$
由方程组$\left\{\begin{array}{l}x=n(y+2)\\{x^2}+4{y^2}=4t\end{array}\right.$,消去x,得
(n2+4)y2+4n2y+4(n2-t)=0,
由韦达定理,得
$\left\{\begin{array}{l}2-\frac{14}{3}=-\frac{{4{n^2}}}{{{n^2}+4}}\\ 2•(-\frac{14}{3})=\frac{{4{n^2}-4t}}{{{n^2}+4}}\end{array}\right.$,
解得$n=±2\sqrt{2},t=36$.
点评 本题考查高次方程,解题的关键是明确题意,找出所求问题需要的条件.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
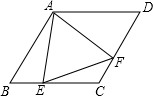 如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
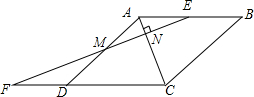 如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.
如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
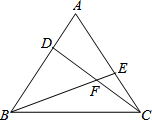 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -30 | C. | -32 | D. | -38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 3 | ||
| y | $\frac{2}{3}$ | 2 | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
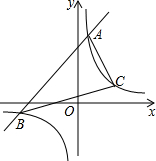 如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;
如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com