
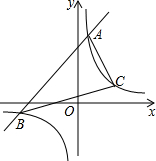
 如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;
如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;分析 (1)判断出点A的横坐标是1,然后利用反比例函数解析式求出点A的坐标,再代入直线解析式计算即可求出b的值,联立两函数解析式,解方程组即可得到点B的坐标;
(2)根据点C到y轴的距离为3得到点C的坐标,构建矩形利用割补法可求三角形面积.
解答 解:(1)∵当x>1时,y1>y2,当0<x<1时,y1<y2,
∴点A的横坐标为1,
又点A在y2=$\frac{6}{x}$上,
∴点A的坐标为(1,6),
将A(1,6)代入y1=x+b得:b=5,
由y=x+5与y=$\frac{6}{x}$联立解得(1,6)或(-6,-1),
∵点B在第三象限,
∴点B的坐标为(-6,-1);
(2)在y=$\frac{6}{x}$中,当x=3时,y=2,
所以△ABC的面积=7×9-$\frac{1}{2}×$9×3-$\frac{1}{2}$×7×7-$\frac{1}{2}$×2×4=21.
点评 本题考查反比例函数与一次函数的交点,主要利用了待定系数法求一次函数解析式,联立两函数解析式求交点坐标,本题难点在于根据函数值的大小判断出点A、B中有一个点的横坐标是1,从而求出交点坐标,这也是解答本题的突破口.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
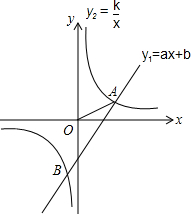 如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.
如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(米) | … | 6.00~6.49 | 6.50~6.99 | 7.00~7.49 | 7.50~7.99 | 8.00~8.49 | 8.50及以上 |
| 得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
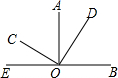 如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )
如图,已知AO⊥OB,CO⊥DO,∠BOC=β°,则∠AOD的度数为( )| A. | β°-90° | B. | 2β°-90° | C. | 180°-β° | D. | 2β°-180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com