
| 成绩(米) | … | 6.00~6.49 | 6.50~6.99 | 7.00~7.49 | 7.50~7.99 | 8.00~8.49 | 8.50及以上 |
| 得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
分析 (1)根据平均数的定义求解;
(2)对照表格得到10名男生实心球得分,然后根据中位线、众数的概念解答;
(3)用样本根据总体.
解答 解:(1)平均数为:$\frac{1}{10}$(7.39+8.6)9+9.41+7.5+8.5+.89+11.11+8.31+6.09+8.11)=8.30(m),
所以这10名男生掷实心球的成绩的平均数是8.30米;
(2)这10名男生掷实心球得分的众数是10分,中位数是9分;
故答案为:10,9;
(3)因为这10名男生掷实心球得分钟9分及以上的共有6人,
所以估计500名男生在本次模拟测试中得优秀的人数为500×$\frac{6}{10}$=300人.
点评 本题考查了平均数,中位线,众数的概念,众数是一组数据中出现次数最多的数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同.


科目:初中数学 来源: 题型:解答题
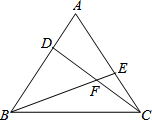 如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.
如图,在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过7分钟后,它们分别爬行到D、E处,设DC与BE的交点为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
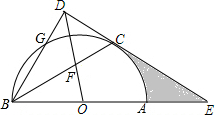 如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
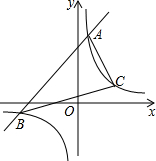 如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;
如图,已知直线y1=x+b与双曲线y2=$\frac{6}{x}$相交于A、B两点,且当x>1时,总有y1>y2;当0<x<1时,总有y1<y2;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
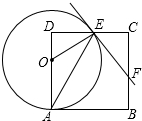 如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com