
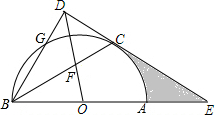
 如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,点C、G是⊙O上两点,且$\widehat{AC}$=$\widehat{CG}$,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.分析 (1)如图1,连接OC,AC,CG,由圆周角定理得到∠ABC=∠CBG,根据同圆的半径相等得到OC=OB,于是得到∠OCB=∠OBC,等量代换得到∠OCB=∠CBG,根据平行线的判定得到OC∥BG,即可得到结论;
(2)①由OC∥BD,得到△OCF∽△BDF,△EOC∽△EBD,根据相似三角形的性质得到$\frac{OC}{BD}$=$\frac{OF}{DF}$=$\frac{2}{3}$,$\frac{OC}{BD}=\frac{OE}{DE}$=$\frac{2}{3}$,根据直角三角形的性质即可得到结论;
②由①的结论得到△OAC是等边三角形,得到∠OAC=60°,根据圆内接四边形的性质得到∠DGC=60°,求得CG=2DG=12,得到AC=CG=12,根据扇形和三角形的面积公式即可得到结论.
解答 (1)证明:如图,连接OC,AC,CG,
∵$\widehat{AC}$=$\widehat{CG}$,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:①∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,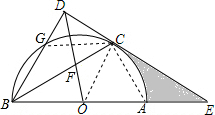
∴$\frac{OC}{BD}$=$\frac{OF}{DF}$=$\frac{2}{3}$,
∴$\frac{OC}{BD}=\frac{OE}{DE}$=$\frac{2}{3}$,
∵OA=OB,
∴AE=OA=OB,
∴OC=$\frac{1}{2}$OE,
∵∠ECO=90°,
∴∠E=30°;
②∵∠E=30°,
∴∠COE=60°,
∵OC=OA,
∴△OAC是等边三角形,
∴∠OAC=60°,
∴∠DGC=60°,
∵∠CDG=90°,DG=6,
∴CG=2DG=12,
∴AC=CG=12,
∴OC=12,CE=12$\sqrt{3}$,
∴S阴影=S△OCE-S扇形AOC=$\frac{1}{2}$×12×12$\sqrt{3}$-$\frac{60π×1{2}^{2}}{360}$=72$\sqrt{3}$-24π.
点评 本题考查了切线的判定和性质,锐角三角函数,勾股定理相似三角形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
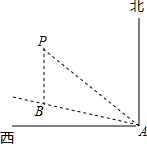 如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?
如图,一艘船以每小时24海里的速度向北偏西75°方向航行,在点A灯处测得灯塔P在船的西北方向,航行40分钟后到达点B处,这时灯塔P恰好在船的正北方向,已知距离灯塔9海里以外的海区为安全航行区域.问:这艘船能否按原方向继续向前航行?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
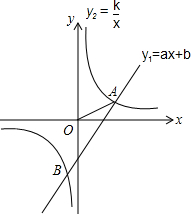 如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.
如图.点A(3,1),B(-1,n)是一次函数y1=ax+b和反比例函数y2=$\frac{k}{x}$图象的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(米) | … | 6.00~6.49 | 6.50~6.99 | 7.00~7.49 | 7.50~7.99 | 8.00~8.49 | 8.50及以上 |
| 得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
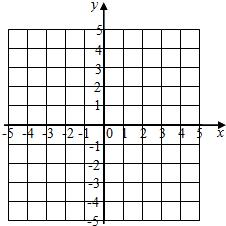 如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.
如图,在平面直角坐标系中,分别描出下列各点A(0,0),B(5,4),C(3,0),D(5,1),E(5,-1),F(4,-2),并按A-B-C-D-E-C-F-A顺序连接起来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com