
| A. | -6 | B. | -30 | C. | -32 | D. | -38 |
分析 分式方程去分母转化为整式方程,分类讨论整式方程只有一个实数根,检验后求出a的值总和即可.
解答 解:已知方程化为2x2+4x+a+8=0①,
若方程①有两个相等实根,则△=16-8(a+8)=0,即a=-6,
当a=-6时,方程①的根x1=x2=-1,符合要求;
若x=2是方程①的根,则8+8+a+8=0,即a=-24,
此时,方程①的另一个根为x=-4,符合要求;
若x=-2是方程①的根,则8-8+a+8=0,即a=-8,
此时方程①的另一个根为x=0,符合要求,
综上,符合条件的a有-6,-24,-8,其总和为-38,
故选D
点评 此题考查了分式方程的解,利用了分类讨论的思想,注意分式方程有解,即最简公分母不能为0.


科目:初中数学 来源: 题型:填空题
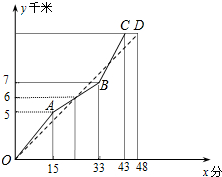 如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.
如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
| 方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com