
【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
(Ⅰ)计算AB的长等于;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明) .
【答案】![]() ;取BC的中点P,在AC上截取AQ=
;取BC的中点P,在AC上截取AQ= ![]() AC,线段PQ即为所求
AC,线段PQ即为所求
【解析】解:(Ⅰ)由图象可知AB= ![]() =
= ![]() .
.
(Ⅱ)设BP=CQ=x,
∵BC= ![]() =
= ![]() ,
,
∴PC= ![]() ﹣x,
﹣x,
在Rt△PCQ中,PQ= ![]() =
= ![]() ,
,
对于函数y=2x2﹣3 ![]() x+
x+ ![]() ,当x=﹣
,当x=﹣ ![]() =
= ![]() 时,y有最小值,此时PQ的值最小,
时,y有最小值,此时PQ的值最小,
此时PC=PB=CQ= ![]() AC.取BC的中点P,在AC上截取AQ=
AC.取BC的中点P,在AC上截取AQ= ![]() AC,图中PQ即为所求.
AC,图中PQ即为所求.

所以答案是:取BC的中点P,在AC上截取AQ= ![]() AC,线段PQ即为所求.
AC,线段PQ即为所求.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图①,将射线Ox按逆时针方向旋转β,得到的射线Oy,如果P为射线Oy上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为(a,β).例如,图②中,如果OM=8,∠xOM=110°,那么点M在平面内的位置记为M(8,110°),根据图形,解答下列问题:
(1)如图③,如果点N在平面内的位置记为N(6,30°),那么ON=__ __,∠xON= .
(2)如果点A,B在平面内的位置分别记为A(5,30°),B(12,120°),求A,B两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnn均为等腰直角三角形,且∠C1=∠C2=∠C3=…=∠n=90°,点A1、A2、A3、…、An和点B1、B2、B3、…、Bn分别在正比例函数y=![]() x和y=﹣x的图象上,且点A1、A2、A3、…、An的横坐标分别为1,2,3…n,线段A1B1、A2B2、A3B3、…、AnBn均与y轴平行.按照图中所反映的规律,则△AnBnn的顶点n的坐标是_____;线段C2018C2019的长是_____.(其中n为正整数)
x和y=﹣x的图象上,且点A1、A2、A3、…、An的横坐标分别为1,2,3…n,线段A1B1、A2B2、A3B3、…、AnBn均与y轴平行.按照图中所反映的规律,则△AnBnn的顶点n的坐标是_____;线段C2018C2019的长是_____.(其中n为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
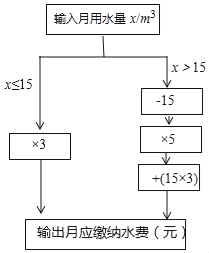
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折, 使点A落在BC边上的点F处,则CE的最大值为( )
A.![]()
B.![]()
C.4
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=![]() ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )

A. ②③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题:
(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式![]() 中,
中,![]() 表示这个多项式的项数,
表示这个多项式的项数,![]() 表示这个多项式中三次项的系数.在数轴上点
表示这个多项式中三次项的系数.在数轴上点![]() 与点
与点![]() 所表示的数恰好可以用
所表示的数恰好可以用![]() 与
与![]() 分别表示.有一个动点
分别表示.有一个动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)![]() ________,
________,![]() ___________,线段
___________,线段![]() _________个单位长度;
_________个单位长度;
(2)点![]() 所表示数是________(用含
所表示数是________(用含![]() 的多项式表示);
的多项式表示);
(3)求当![]() 为多少时,线段
为多少时,线段![]() 的长度恰好是线段
的长度恰好是线段![]() 长度的三倍?
长度的三倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com