
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求 ![]() 的值.
的值.
【答案】
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=ABAD.
(2)证明:∵E为AB的中点,∠ACB=90°,
∴CE= ![]() AB=AE.
AB=AE.
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
∴AD∥CE
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE= ![]() AB,
AB,
∴CE= ![]() ×7=
×7= ![]() ,
,
∵AD=5,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
【解析】(1)首先证明△ADC∽△ACB,然后依据相似三角形的对应边成比例得到AC2=ABAD;
(2)根据在直角三角形中,斜边上的中线等于斜边的一半可证得CE=![]() ,AB=AE,然后依据等边对等角的性质可得到∠EAC=∠ECA.通过等量代换可得到∠DAC=∠ECA,故此可证明CE∥AD;
,AB=AE,然后依据等边对等角的性质可得到∠EAC=∠ECA.通过等量代换可得到∠DAC=∠ECA,故此可证明CE∥AD;
(3)首先证明△AFD∽△CFE,然后由相似三角形的对应边成比例的性质可求得![]() 的值.
的值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E、F分别是AD、AB的中点,EF交AC于点G,那么AG:GC的值为( )
A.1:2
B.1:3
C.1:4
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,时钟是我们常见的生活必需品,其中蕴含着许多数学知识.

(1)我们知道,分针和时针转动一周都是 度,分针转动一周是 分钟,时针转动一周有12小时,等于720分钟;所以,分针每分钟转动 度,时针每分钟转动 度.
(2)从5:00到5:30,分针与时针各转动了多少度?
(3)请你用方程知识解释:从1:00开始,在1:00到2:00之间,是否存在某个时刻,时针与分针在同一条直线上?若不存在,说明理由;若存在,求出从1:00开始经过多长时间,时针与分针在同一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,妈妈下班后从公司开车回家,途中想起忘了带第二天早上开早会的一个文件夹,于是打电话让办公室王阿姨马上从公司送来,同时妈妈也往回开,遇到王阿姨后停下说了几句话,接着继续开车回家.设妈妈从公司出发后所用时间为t,妈妈与家的距离为s.下面能反映s与t的函数关系的大致图象是( )
A.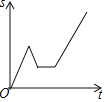 B.
B.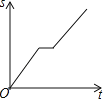
C. D.
D.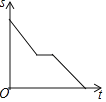
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )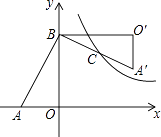
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程组:①![]() ②
②![]() ③
③![]() ④
④![]() ,比较适宜的方法是( )
,比较适宜的方法是( )
A.①②用代入法,③④用加减法B.①③用代入法,②④用加减法
C.②③用代入法,①④用加减法D.②④用代入法,①③用加减法
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com