
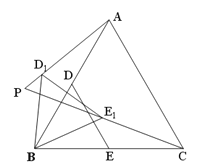
【题目】已知:在等边△ABC中, AB=![]() , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
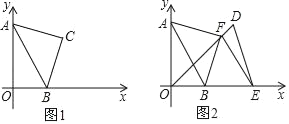
【题目】在平面直角坐标系中,点A(0,a)、B(b,0).
(1)若a、b满足a2+b2﹣8a﹣4b+20=0.如图,在第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;
(2)如图,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=﹣0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段DE上一个动点(P不与D,E重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A,B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
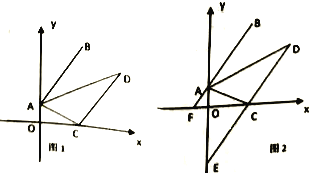
【题目】如图1,在平面直角坐标系中,![]() ,将线段
,将线段![]() 平移得到线段
平移得到线段![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连结
,连结![]() .
.
(1)点![]() 的坐标为__________________(用含
的坐标为__________________(用含![]() 的式子表示);
的式子表示);
(2)若![]() 的面积为4,求点
的面积为4,求点![]() 的坐标;
的坐标;
(3)如图2,在(2)的条件下,延长![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于
轴于![]() ,
,![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的值记为
的值记为![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的值是否发生变化,若不变,请求出
的值是否发生变化,若不变,请求出![]() 的值,并写出此时
的值,并写出此时![]() 的取值范围,若变化,说明理由.
的取值范围,若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
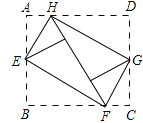
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=40°,点C在OA上,点P为OB上一动点,∠CPB的角平分线PD交射线OA于D。设∠OCP的度数为x°,∠CDP的度数为y°。

小明对x与y之间满足的等量关系进行了探究,
下面是小明的探究过程,请补充完整;
(1)x的取值范围是 ;
(2)按照下表中x的值进行取点、画图、计算,分别得到了y与x的几组对应值,补全表格;

(3)在平面直角坐标系xOy中,
①描出表中各组数值所对应的点(x,y);
②描出当x=120°时,y的值;
(4)若∠AOB=![]() °,题目中的其它条件不变,用含
°,题目中的其它条件不变,用含![]() 、x的代数式表示y为 。
、x的代数式表示y为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
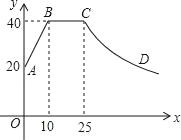
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
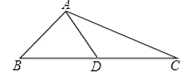
【题目】如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化作整式与真分式的和的形式.
如:![]() ;
;![]()
(1)下列分式中,属于真分式的是__________(填序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)将假分式![]() 化为整式与真分式的和的形式:
化为整式与真分式的和的形式:![]() __________;若假分式
__________;若假分式![]() 的值为正整数,则整数
的值为正整数,则整数![]() 的值为__________;
的值为__________;
(3)请你写出假分式![]() 化成整式与真分式的和的形式的完整过程.
化成整式与真分式的和的形式的完整过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com