
【题目】如图,抛物线m:y=﹣0.25(x+h)2+k与x轴的交点为A,B,与y轴的交点为C,顶点为M(3,6.25),将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D.
(1)求抛物线n的解析式;
(2)设抛物线n与x轴的另一个交点为E,点P是线段DE上一个动点(P不与D,E重合),过点P作y轴的垂线,垂足为F,连接EF.如果P点的坐标为(x,y),△PEF的面积为S,求S与x的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)设抛物线m的对称轴与x轴的交点为G,以G为圆心,A,B两点间的距离为直径作⊙G,试判断直线CM与⊙G的位置关系,并说明理由.

【答案】(1)y=![]() x2﹣
x2﹣![]() x+36;(2)S=﹣
x+36;(2)S=﹣![]() x2+
x2+![]() x(13<x<18),△PEF的面积S没有最大值;(3)直线CM与⊙G相切,理由见解析.
x(13<x<18),△PEF的面积S没有最大值;(3)直线CM与⊙G相切,理由见解析.
【解析】试题分析:(1)根据抛物线m的顶点为M(3,6.25)得出m的解析式为y=-![]() (x-3)2+
(x-3)2+![]() =-
=-![]() (x-8)(x+2),求出A(-2,0),B(8,0),再根据旋转的性质得出D的坐标为(13,-6.25),进而求出抛物线n的解析式;
(x-8)(x+2),求出A(-2,0),B(8,0),再根据旋转的性质得出D的坐标为(13,-6.25),进而求出抛物线n的解析式;
(2)由点E与点A关于点B成中心对称,得出E(18,0),利用待定系数法求出直线DE的解析式为y=![]() x-
x-![]() ,再根据S△PEF=
,再根据S△PEF=![]() PFOF得出S与x的函数关系式,进而求解即可;
PFOF得出S与x的函数关系式,进而求解即可;
(3)利用勾股定理求出CG=![]() =5=⊙G的半径,得出点C在⊙G上.过M作y轴的垂线,垂足为N,连结CM,利用勾股定理求出CM2=CN2+MN2=(
=5=⊙G的半径,得出点C在⊙G上.过M作y轴的垂线,垂足为N,连结CM,利用勾股定理求出CM2=CN2+MN2=(![]() -4)2+32=
-4)2+32=![]() ,计算得出CG2+CM2=52+
,计算得出CG2+CM2=52+![]() =
=![]() =(
=(![]() )2=GM2,根据勾股定理的逆定理得到CG⊥CM,由切线的判定定理即可得出直线CM与⊙G相切.
)2=GM2,根据勾股定理的逆定理得到CG⊥CM,由切线的判定定理即可得出直线CM与⊙G相切.
试题解析:(1)∵抛物线m:y=﹣0.25(x+h)2+k的顶点为M(3,6.25),
∴m的解析式为y=﹣![]() (x﹣3)2+
(x﹣3)2+![]() =﹣
=﹣![]() (x﹣8)(x+2),
(x﹣8)(x+2),
∴A(﹣2,0),B(8,0),
∵将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为D,
∴D的坐标为(13,﹣6.25),
∴抛物线n的解析式为y=![]() (x﹣13)2﹣
(x﹣13)2﹣![]() ,即y=
,即y=![]() x2﹣
x2﹣![]() x+36;
x+36;
(2)∵点E与点A关于点B成中心对称,
∴E(18,0).
设直线DE的解析式为y=kx+b,
则 ,解得
,解得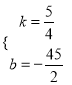
∴y=![]() x﹣
x﹣![]() ,
,
∵P点的坐标为(x,y),13<x<18,
∴S△PEF=![]() PFOF=
PFOF=![]() x(﹣y)=﹣
x(﹣y)=﹣![]() xy=﹣
xy=﹣![]() x(
x(![]() x﹣
x﹣![]() )=﹣
)=﹣![]() x2+
x2+![]() x,
x,
即S=﹣![]() x2+
x2+![]() x(13<x<18),
x(13<x<18),
∴当x= =9时,S有最大值,但13<x<18,所以△PEF的面积S没有最大值;
=9时,S有最大值,但13<x<18,所以△PEF的面积S没有最大值;
(3)直线CM与⊙G相切,理由如下:
∵抛物线m的解析式为y=﹣![]() (x﹣3)2+
(x﹣3)2+![]() =﹣
=﹣![]() (x﹣8)(x+2),
(x﹣8)(x+2),
∴令x=0,得y=4,
∴C(0,4).
∵抛物线m的对称轴与x轴的交点为G,
∴G(3,0),
∵OC=4,OG=3,连结CG,
∴CG=![]() =5,
=5,
∵AB=10,
∴⊙G的半径是5,
∴点C在⊙G上.
过M作y轴的垂线,垂足为N,连结CM,
则CM2=CN2+MN2=(![]() ﹣4)2+32=
﹣4)2+32=![]() ,
,
又CG2+CM2=52+![]() =
=![]() =(
=(![]() )2=GM2,
)2=GM2,
∴CG⊥CM,
∴直线CM与⊙G相切.



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个![]() 的小方格的正方形 雷区中,随机埋藏着
的小方格的正方形 雷区中,随机埋藏着![]() 颗地雷,每个小方格内最多只能埋藏
颗地雷,每个小方格内最多只能埋藏![]() 颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“
颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“![]() ”,其意义表示该格的外围区域(图中阴影部分,记为
”,其意义表示该格的外围区域(图中阴影部分,记为![]() 区域)有
区域)有![]() 颗地雷;接着小红又点击了左上角第一个方格,出现了数字“
颗地雷;接着小红又点击了左上角第一个方格,出现了数字“![]() ”,其外围区域(图中阴影)记为
”,其外围区域(图中阴影)记为![]() 区域;
区域;![]() 区域与
区域与![]() 区域以及出现数字“
区域以及出现数字“![]() ”和“
”和“![]() ”两格以外的部分记为
”两格以外的部分记为![]() 区域。请分别计算出
区域。请分别计算出![]() 区、
区、![]() 区、
区、![]() 区点中地雷的概率,那么她应点击
区点中地雷的概率,那么她应点击![]() 、
、![]() 、
、![]() 中的哪个区域?
中的哪个区域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的高为16m,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为 60°,在楼顶B处测得塔顶D处的仰角为45°,其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高.(![]() =1.73,结果保留一位小数.)
=1.73,结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题
(1)抽取了______名学生成绩;(2)请把条形统计图补充完整;
(3)扇形统计图中等级D所在的扇形的圆心角度数是______;
(4)若A,B,C代表合格,该校初二年级有300名学生,求全年级生物合格的学生共约多少人

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A. ![]() B. 5C. 3D.
B. 5C. 3D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
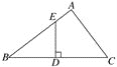
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
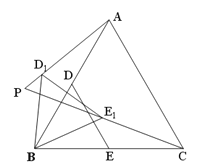
【题目】已知:在等边△ABC中, AB=![]() , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(1﹣2k)x2﹣2![]() x﹣1=0
x﹣1=0
(1)若此方程为一元一次方程,求k的值.
(2)若此方程为一元二次方程,且有实数根,试求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com