
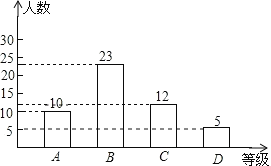
����Ŀ��ijУ���꼶ѧ��ȫ���μ���������������ῼ�������г�ȡ�˲���ѧ��������Գɼ��������ǵijɼ�����ͳ�ƺ��ΪA��B��C��D�ĵȣ�����ͳ�ƽ�����Ƴ����µ�ͳ��ͼ������ͼ����������Ϣ�����������
��1����ȡ��______��ѧ���ɼ�����2���������ͳ��ͼ����������
��3������ͳ��ͼ�еȼ�D���ڵ����ε�Բ�ĽǶ�����______��
��4����A��B��C�����ϸ�У�����꼶��300��ѧ������ȫ�꼶����ϸ��ѧ����Լ������

���𰸡���1��50��2����������3��36��4��270
��������
(1)����B�ȼ��������Լ���ռ�İٷֱȼ�����ó�ȡ��ѧ������
(2)���D�ȼ���������ȫ����ͳ��ͼ���ɣ�
(3)��D�ȼ���ռ�ı�������360�ȼ��ɵã�
(4)��300����A��B��C�����ȼ���ռ�ı����ĺͼ��ɵ�.
(1)��������ã�23��46%=50(��)��
���ȡ��50��ѧ���ɼ���
�ʴ�Ϊ��50��
(2)D�ȼ���ѧ����50-(10+23+12)=5(��)��
��ȫͼ�Σ���ͼ��ʾ��
(3)��������ã�![]() ��360��=36�㣬
��360��=36�㣬
�ʴ�Ϊ��36�㣻
(4)��������ã�300��![]() =270(��)��
=270(��)��
��ȫ�꼶����ϸ��ѧ����Լ270�ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A��60����AD��8��F��AB���е㣮����F��FE��AD������ΪE.����AEF�ص�A����B�ķ���ƽ�ƣ��õ���A��E��F��.��P��P���ֱ���EF��E��F�����е㣬����A�����B�غ�ʱ���ı���PP��F��F�����Ϊ( ����)

A. 8![]() B. 4
B. 4![]() C. 12
C. 12![]() D. 8
D. 8![]() ��8
��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ���ĸ��ֱ��������1��2��3��4��С�����ǵ���״����С���ʵص���ȫ��ͬ��С���ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy��
��1�����б�����ʾ����x��y�������п��ܳ��ֵĽ����
��2����С����С����ȡһ��С����ȷ���ĵ㣨x��y�����ڷ���������y=![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
��3����С����С����ȡһ��С����ȷ������x��y����y��![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AEFG�Ķ���E��G�ֱ���������ABCD��AB��AD���ϣ�����B����EF�ڵ�M����FG�ڵ�N����AE=a��AG=b��AB=c��b��a��c����
��1����֤�� ![]() ��
��
��2������AMN���������a��b��c�Ĵ���ʽ��ʾ����
��3������MAN=45��ʱ����֤��c2=2ab��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
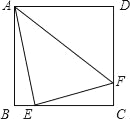
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ����AE=4��EF=3��AF=5����ô������ABCD���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������m��y=��0.25��x+h��2+k��x��Ľ���ΪA��B����y��Ľ���ΪC������ΪM��3��6.25������������m�Ƶ�B��ת180�����õ��µ�������n�����Ķ���ΪD��
��1����������n�Ľ���ʽ��
��2����������n��x�����һ������ΪE����P���߶�DE��һ�����㣨P����D��E�غϣ�������P��y��Ĵ��ߣ�����ΪF������EF�����P�������Ϊ��x��y������PEF�����ΪS����S��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ�������S�����ֵ��
��3����������m�ĶԳ�����x��Ľ���ΪG����GΪԲ�ģ�A��B�����ľ���Ϊֱ������G�����ж�ֱ��CM���G��λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ǰѶԽ�����ȵ��ı��ν��������ı��Σ�
![]() ��ٳ�һ������ѧ���������ı������Ǻ����ı��ε����ӣ�
��ٳ�һ������ѧ���������ı������Ǻ����ı��ε����ӣ�
![]() ��ͼ1��E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��DA���е㣬��֪�ı���EFGH�����Σ���֤���ı���ABCD�Ǻ����ı��Σ�
��ͼ1��E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��DA���е㣬��֪�ı���EFGH�����Σ���֤���ı���ABCD�Ǻ����ı��Σ�
![]() ��ͼ2���ı���ABCD�Ǻ����ı��Σ��Խ���AC��BD�ཻ��O��
��ͼ2���ı���ABCD�Ǻ����ı��Σ��Խ���AC��BD�ཻ��O��![]() ��E��F�ֱ���AD��BC���е㣬��̽��EF��AC֮���������ϵ����֤����Ľ��ۣ�
��E��F�ֱ���AD��BC���е㣬��̽��EF��AC֮���������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD���ĸ�����������ǡ��ƴ��һ����϶���ص����ı���EFGH��EH=12���ף�EF=16���ף����AD�ij��ǣ�������
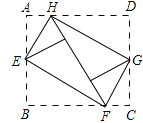
A. 12���� B. 16���� C. 20���� D. 28����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
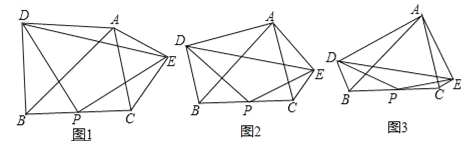
����Ŀ����֪����ABC������BAC=60������PΪ��BC���е����ֱ���AB��ACΪб��������Rt��ABD��Rt��ACE������DAB=��EAC=��������PD��PE��DE��
��1����ͼ1������=45������![]() =�� ����
=�� ����
��2����ͼ2������Ϊ����Ƕ�����֤����PDE=����
��3����ͼ3������=15����AB=8��AC=6������PDE�����Ϊ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com