
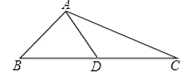
【题目】如图,在△ABC中,AB=5,AC=13,边BC上的中线AD=6.
(1)以点D为对称中心,作出△ABD的中心对称图形;
(2)求点A到BC的距离.
【答案】解析】
(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)旋转180°得到的图形和原图形中心对称.(2) 作AM⊥BC于M,利用全等,三角形AEC,ABC等面积, ![]() AMBD=
AMBD= ![]() ABAD,求AM的长度.
ABAD,求AM的长度.
试题解析:
解:(1)如图,△DCE即为所求.
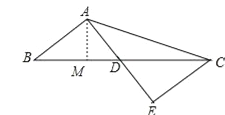
(2)作AM⊥BC于M,如图,AE=AD+DE=6+6=12,
∵△ABD与△ECD关于点D中心对称,
∴CE=AB=5,在△ACE中,
∵CE=5,AE=12,AC=13,而52+122=132,
∴CE2+AE2=AC2,
∴△ACE为直角三角形,∠AEC=90°,
∴∠BAD=∠AEC=90°,在Rt△ABD中,BD=![]() ,
,
∵![]() AMBD=
AMBD= ![]() ABAD,
ABAD,
∴AM =![]() ,即点A到BC的距离为
,即点A到BC的距离为![]() .
.


科目:初中数学 来源: 题型:
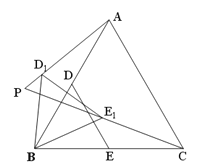
【题目】已知:在等边△ABC中, AB=![]() , D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
, D,E分别是AB,BC的中点(如图).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.点P到BC所在直线的距离的最大值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
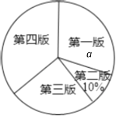
各版面选择人数的扇形统计图
各版面选择人数的条形统计图
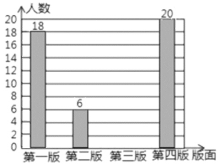
请根据图中信息,解答下列问题:
(1)a=______%,“第四版”对应扇形的圆心角为 °;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=![]() (x>0)与y2=
(x>0)与y2=![]() (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(1﹣2k)x2﹣2![]() x﹣1=0
x﹣1=0
(1)若此方程为一元一次方程,求k的值.
(2)若此方程为一元二次方程,且有实数根,试求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合。将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.

(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com