
ЁОЬтФПЁПМзЁЂввСНАрЗжБ№бЁ5УћЭЌбЇзщГЩДњБэЖгВЮМгбЇаЃзщжЏЕФЁАЙњЗРжЊЪЖЁБбЁАЮШќЃЌЯжИљОнГЩМЈЃЈТњЗж10ЗжЃЉжЦзїШчЭМЭГМЦЭМКЭЭГМЦБэЃЈЩаЮДЭъГЩЃЉ
МзЁЂввСНАрДњБэЖгГЩМЈЭГМЦБэ
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю | |
МзАр | 8.5 | 8.5 | a | 0.7 |
ввАр | 8.5 | b | 10 | 1.6 |
ЧыИљОнгаЙиаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉбЇаЃдЄЙРШчЙћЦНОљЗжФмДя8.5ЗжЃЌдкВЮМгЪаЭХЬхБШШќжаМДПЩвдЛёНБЃЌЯжгІбЁХЩЁЁ ЁЁДњБэЖгВЮМгЪаБШШќЃЛЃЈЬюЁАМзЁБЛђЁАввЁБЃЉ
ЃЈ3ЃЉЯжНЋДгГЩМЈТњЗжЕФ3ИібЇЩњжаЫцЛњГщШЁ2ШЫВЮМгЪаЙњЗРжЊЪЖИіШЫОКШќЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЧЁКУГщЕНМзЃЌввАрИївЛИібЇЩњЕФИХТЪЃЎ
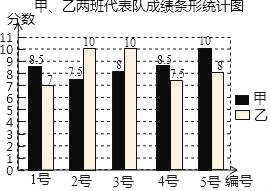
ЁОД№АИЁПЃЈ1ЃЉ8.5ЃЌbЃН8ЃЛЃЈ2ЃЉМзАр;ЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЬѕаЮЭГМЦЭМЃЌНсКЯжкЪ§ЁЂжаЮЛЪ§ЕФЖЈвхЗжБ№ЧѓГіД№АИЃЛ
ЃЈ2ЃЉРћгУЦНОљЪ§ЁЂЗНВюЕФЖЈвхЗжЮіЕУГіД№АИЃЛ
ЃЈ3ЃЉЪзЯШИљОнЬтвтСаБэЃЌШЛКѓгЩСаБэЧѓЕУЫљгаЕШПЩФмЕФНсЙћгыЧЁКУГщЕНМзЃЌввАрИївЛИібЇЩњЕФЧщПіЃЌдйРћгУИХТЪЙЋЪНЧѓНтМДПЩЧѓЕУД№АИЃЎ
НтЃКЃЈ1ЃЉМзЕФжкЪ§ЮЊЃК8.5ЃЌввЕФжаЮЛЪ§ЮЊЃК8ЃЌ
ЙЪД№АИЮЊЃК8.5ЃЌ8ЃЛ
ЃЈ2ЃЉДгЦНОљЪ§ПДЃЌСНАрЦНОљЪ§ЯрЭЌЃЌдђМзЁЂввСНАрЕФГЩМЈвЛбљКУЃЛ
ДгЗНВюПДЃЌМзАрЕФЗНВюаЁЃЌЫљвдМзАрЕФГЩМЈИќЮШЖЈЃЎ
ЙЪД№АИЮЊЃКМзАрЃЛ
ЃЈ3ЃЉСаБэШчЯТЃК
Мз | вв1 | вв2 | |
Мз | ЉЉЉ | вв1 Мз | вв2 Мз |
вв1 | Мз вв1 | ЉЉЉ | вв2вв1 |
вв2 | Мз вв2 | вв1вв2 | ЉЉЉ |
ЫљгаЕШПЩФмЕФНсЙћЮЊ6жжЃЌЦфжаГщЕНМзАрЁЂввАрИївЛШЫЕФНсЙћЮЊ4жжЃЌ
ЫљвдPЃЈГщЕНAЃЌBЃЉЃН![]() ЃЎ
ЃЎ


 аЁбЇЖсЙкABОэЯЕСаД№АИ
аЁбЇЖсЙкABОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019ФъзуЧђбЧжоБе§дкАЂСЊЧѕНјааЃЌетЯюЦ№дДгкЮвЙњЁАѕэОЯЁБЕФдЫЖЏЯюФПНќФъРДдкЮвЙњжааЁбЇаЃдАЕУЕНДѓСІЭЦЙуЃЌФГДЮаЃдАзуЧђБШШќЙцЖЈЃКЪЄвЛГЁЕУ3ЗжЃЌЦНвЛГЁЕУ1ЗжЃЌИКвЛГЁЕУ0ЗжЃЌФГзуЧђЖгЙВНјааСЫ8ГЁБШШќЃЌЕУСЫ12ЗжЃЌИУЖгЛёЪЄЕФГЁЪ§гаМИжжПЩФмЃЈЁЁЁЁЃЉ
A. 3B. 4C. 5D. 6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
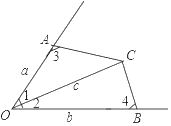
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮAOBCжаЃЌШєЁЯ1ЃНЁЯ2ЃЌЁЯ3+ЁЯ4ЃН180ЁуЃЌдђЯТСаНсТле§ШЗЕФгаЃЈЁЁЁЁЃЉ
ЃЈ1ЃЉAЁЂOЁЂBЁЂCЫФЕуЙВдВ
ЃЈ2ЃЉACЃНBC
ЃЈ3ЃЉcosЁЯ1ЃН![]()
ЃЈ4ЃЉSЫФБпаЮAOBCЃН![]()
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЮЊЦНааЫФБпаЮABCDБпADЩЯвЛЕуЃЌEЁЂFЗжБ№ЮЊPBЁЂPCЕФжаЕуЃЌЁїPEFЁЂЁїPDCЁЂЁїPABЕФУцЛ§ЗжБ№ЮЊSЁЂS1ЁЂS2ЃЌШєS=2ЃЌдђS1+S2=ЃЈ ЃЉ

A. 4 B. 6 C. 8 D. ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЪЧЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌСЌНгOAЃЌШєНЋЯпЖЮO AШЦЕуOЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮOBЃЌдђЕуBЫљдкЭМЯѓЕФКЏЪ§БэДяЪНЮЊ______ЃЎ
ЕФЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌСЌНгOAЃЌШєНЋЯпЖЮO AШЦЕуOЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮOBЃЌдђЕуBЫљдкЭМЯѓЕФКЏЪ§БэДяЪНЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
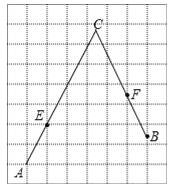
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌAЃЌEЮЊИёЕуЃЌBЃЌFЮЊаЁе§ЗНаЮБпЕФжаЕуЃЌCЮЊAEЃЌBFЕФбгГЄЯпЕФНЛЕуЃЎ
ЃЈЂёЃЉAEЕФГЄЕШгк ЃЛ
ЃЈЂђЃЉШєЕуPдкЯпЖЮACЩЯЃЌЕуQдкЯпЖЮBCЩЯЃЌЧвТњзуAP=PQ=QBЃЌЧыдкШчЭМЫљЪОЕФЭјИёжаЃЌгУЮоПЬЖШЕФжБГпЃЌЛГіЯпЖЮPQЃЌВЂМђвЊЫЕУїЕуPЃЌQЕФЮЛжУЪЧШчКЮевЕНЕФЃЈВЛвЊЧѓжЄУїЃЉ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
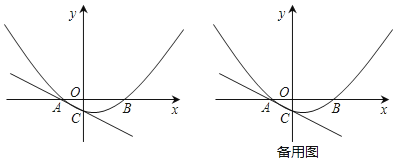
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпy=ax2+bxЉ1Й§AЁЂBСНЕуЃЌВЂгыЙ§AЕуЕФжБЯпy=Љ![]() xЉ1НЛгкЕуCЃЎ
xЉ1НЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАЖдГЦжсЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЫФБпаЮACPOЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕуMЮЊyжсгвВрХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуMзїжБЯпACЕФДЙЯпЃЌДЙзуЮЊNЃЎЮЪЃКЪЧЗёДцдкетбљЕФЕуNЃЌЪЙвдЕуMЁЂNЁЂCЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌШєДцдкЃЌЧѓГіЕуNЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
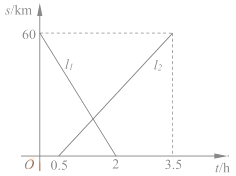
ЁОЬтФПЁПAЁЂBСНЕиЯрОр60kmЃЌМзЁЂввСНШЫДгСНЕиГіЗЂЯрЯђЖјааЃЌМзЯШГіЗЂЃЎЭМжа![]() БэЪОСНШЫРыAЕиЕФОрРыSЃЈkmЃЉгыЪБМфtЃЈhЃЉЕФЙиЯЕЃЌНсКЯЭМЯёЛиД№ЯТСаЮЪЬтЃК
БэЪОСНШЫРыAЕиЕФОрРыSЃЈkmЃЉгыЪБМфtЃЈhЃЉЕФЙиЯЕЃЌНсКЯЭМЯёЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэЪОввРыПЊAЕиЕФОрРыгыЪБМфЙиЯЕЕФЭМЯёЪЧ________(Ью![]() ЃЉЃЛ
ЃЉЃЛ
МзЕФЫйЖШЪЧ__________km/hЃЛввЕФЫйЖШЪЧ________km/hЁЃ
ЃЈ2ЃЉМзГіЗЂКѓЖрЩйЪБМфСНШЫЧЁКУЯрОр5kmЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
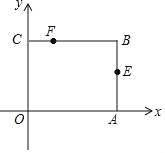
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЗХдквдOЮЊдЕуЕФЦНУцжБНЧзјБъЯЕжаЃЌA(3ЃЌ0)ЃЌC(0ЃЌ2)ЃЌЕуEЪЧABЕФжаЕуЃЌЕуFдкBCБпЩЯЃЌЧвCFЃН1ЃЌШєMЮЊxжсЩЯЕФЖЏЕуЃЌNЮЊyжсЩЯЕФЖЏЕуЃЌдђЫФБпаЮMNFEЕФжмГЄзюаЁжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com