
【题目】二次函数的图象过点(4,-5)和(0,3),且与x轴交于点M(-1,0)和N,
(1)求此二次函数的解析式;
(2)如果这二次函数的图像的顶点为点P,点O是坐标原点,求△OPN的面积.
(3)如果点R与点P关于x轴对称,判定以M、N、P、R为顶点的四边形的边之间的位置与度量关系.
【答案】(1)y=-x2+2x+3;(2)6;(3)该四边形(两组)对边(分别)平行,四条边都相等
【解析】
(1)将已知的三点代入,利用待定系数法即可解答;
(2)先求得点P和点N的坐标,再得出线段ON的长度以及ON边上的高,最后运用三角形面积公式解答即可;
(3)先画出图形,再说明四边形MRNP是菱形,然后运用菱形的性质解答即可.
解:(1)设二次函数的解析式为y=ax2+bx+c,
∴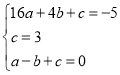 ,
,
可以解得a=-1,b=2,c=3 .
∴y=-x2+2x+3;
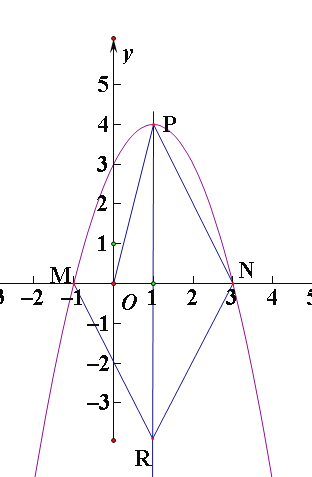
(2)如图:由题意可知二次函数的图像的顶点为点P(1,4),点N(3,0),
∴ON=3, ON边上的高为4
∴S△OPN=3×4÷2=6 .
(3)如图:∵点R与点P关于x轴对称
∴MN垂直平分PR
∵PR是二次函数的图像对称轴
∴PR垂直平分MN
∴PR互相MN垂直平分,
∴PMRN为菱形
∴该四边形(两组)对边(分别)平行,四条边都相等


科目:初中数学 来源: 题型:
【题目】如图1,该抛物线是由y=x2平移后得到,它的顶点坐标为(﹣![]() ,﹣
,﹣![]() ),并与坐标轴分别交于A,B,C三点.
),并与坐标轴分别交于A,B,C三点.
(1)求A,B的坐标.
(2)如图2,连接BC,AC,在第三象限的抛物线上有一点P,使∠PCA=∠BCO,求点P的坐标.
(3)如图3,直线y=ax+b(b<0)与该抛物线分别交于P,G两点,连接BP,BG分别交y轴于点D,E.若ODOE=3,请探索a与b的数量关系.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组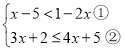
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
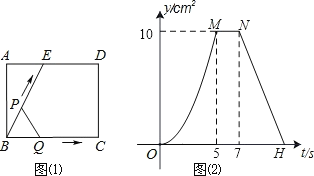
【题目】如图(1)所示,E是矩形ABCD的边AD上一边,动点P,Q同时从点B出发,点P沿折线![]() 运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P,Q同时出发t秒后时,
运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P,Q同时出发t秒后时,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数关系图像如图(2)(曲线OM为抛物线的一部分),则当t的值是___________时,
的函数关系图像如图(2)(曲线OM为抛物线的一部分),则当t的值是___________时,![]() 面积为4.
面积为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
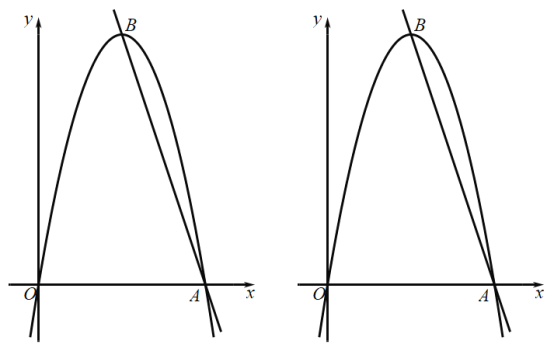
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的正半轴交于点A,抛物线的顶点为B,直线
轴的正半轴交于点A,抛物线的顶点为B,直线![]() 经过A,B两点,且
经过A,B两点,且![]() .
.
(1)求抛物线的解析式
(2)点P在第一象限内对称轴右侧的抛物线上,其横坐标为![]() ,连接OP,交对称轴于点C,过点C作
,连接OP,交对称轴于点C,过点C作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点F,点G是BE的中点,过点G作
于点F,点G是BE的中点,过点G作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 且
且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某扶贫工作队为一贫困户提供了![]() 万元的无息脱贫贷款.该贫困户利用这笔贷款,注册了一家网店,销售一种成本价为
万元的无息脱贫贷款.该贫困户利用这笔贷款,注册了一家网店,销售一种成本价为![]() 元/件的农产品.已知销售价高于成本价,且不高于
元/件的农产品.已知销售价高于成本价,且不高于![]() 元/件,网店每月需支付电费等其它费用
元/件,网店每月需支付电费等其它费用![]() 千元市场调查发现,该农产品每月销售量为
千元市场调查发现,该农产品每月销售量为![]() (百件)与销售价
(百件)与销售价![]() (元/件)之间的函数关系如图所示
(元/件)之间的函数关系如图所示
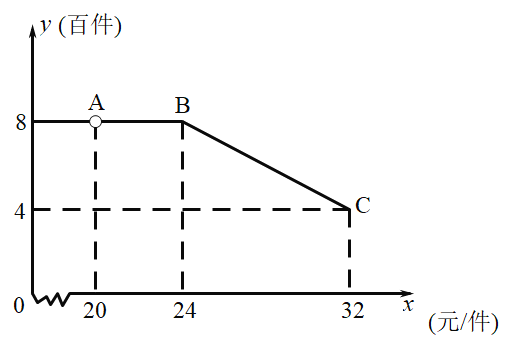
(1)求该网店每月利润![]() (百元)与销售价
(百元)与销售价![]() (元/件)之间的函数关系式,并注明自变量
(元/件)之间的函数关系式,并注明自变量![]() 的取值范围:
的取值范围:
(2)该贫困户从网店开业起,最快在第几个月可用销售利润还清无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中学校每个年级学生刚好为500人,为了解数学史知识的普及情况,随机从每个年级各抽10名学生进行测试,测试成绩整理如下:
年级 | 学生测试成绩表 | |||||||||
七年级 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
八年级 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
九年级 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求每个年级恰好都有一名学生参加的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上两点,且![]() ,连接OC,BD,OD.
,连接OC,BD,OD.
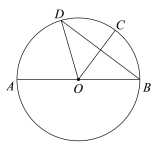
(1)求证:OC垂直平分BD;
(2)过点C作⊙O的切线交AB的延长线于点E,连接AD,CD.
①依题意补全图形;
②若AD=6,![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
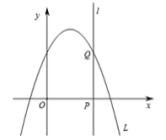
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.
(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com