
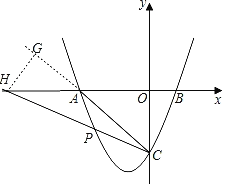
����Ŀ����ͼ1��������������y��x2ƽ�ƺ�õ������Ķ�������Ϊ����![]() ����
����![]() ��������������ֱ���A��B��C���㣮
��������������ֱ���A��B��C���㣮
��1����A��B�����꣮
��2����ͼ2������BC��AC���ڵ�����������������һ��P��ʹ��PCA����BCO�����P�����꣮
��3����ͼ3��ֱ��y��ax+b��b��0����������߷ֱ���P��G���㣬����BP��BG�ֱ�y���ڵ�D��E����ODOE��3����̽��a��b��������ϵ����˵�����ɣ�

���𰸡���1��![]() ����2��
����2��![]() ����3��b��4a+3�����ɼ�������
����3��b��4a+3�����ɼ�������
��������
��1�����ݶ�������д������ʽ��������ʽΪһ��ʽ���ֱ���x=0��y=0�������A��B�����ꣻ
��2��ֱ��CP��x���ڵ�H���ʵ�H��HG��AC��AC���ӳ����ڵ�G������tan��BCO��tan��PCA��ֱ�������μ������H�����꣬�ɴ˿����ֱ��CH�ı���ʽ���������κ�������ʽ������õ�P���ꣻ
��3��ֱ��BP�ı���ʽΪ��y=��m+4��x-��m+4����ֱ��BG�ı���ʽΪ��y=��n+4��x-��n+4������OD=-��m+4����OE=��n+4����ODOE=-��m+4����n+4��=3����-[mn+4��m+n��+16]=3����m+n=a-3��mn=-b-4��������⣮
�⣺��1�������ߵı���ʽΪ��y����x+![]() ��2��
��2��![]() ��x2+3x��4���٣�
��x2+3x��4���٣�
��x��0����y����4���ʵ�C��0����4����
��y��0����x��-4��1��
�ʵ�A��B������ֱ�Ϊ������4��0������1��0����
��2����ͼ����ֱ��CP��x���ڵ�H���ʵ�H��HG��AC��AC���ӳ����ڵ�G��
tan��BCO��![]() ��
��![]() ��tan��PCA��
��tan��PCA��
��OA��OC��4���ʡ�BAC��45������GAH��
��GH��GA��x����GC��4x����AC��GC��GA��3x��4![]() ��
��
��ã�x��![]() ��
��
��AH��![]() x��
x��![]() ���ʵ�H����
���ʵ�H����![]() ��0����
��0����
��CH�ı���ʽΪ��y��kx+b��
��C��H����������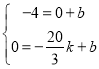 �����
�����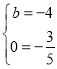 ��
��
��CH�ı���ʽΪ��y����![]() x��4��
x��4��
�����٢ڲ���ã�x��0����ȥ����![]() ��
��
�ʵ�P����![]() ����
����![]() ����
����
��3�����P��G������ֱ�Ϊ����m��m2+3m��4������n��n2+3n��4����
�ɵ�P��B������ã�ֱ��PB�ı���ʽΪ��y����m+4��x����m+4����
ͬ��ֱ��BG�ı���ʽΪ��y����n+4��x����n+4����
��OD������m+4����OE����n+4����
ֱ��y��ax+b��b��0�����ۣ�
�����٢۲������ã�x2+��3��a��x��b��4��0��
��m+n��a��3��mn����b��4��
ODOE������m+4����n+4����3��
����[mn+4��m+n��+16]��3����m+n��a��3��mn����b��4��
�����ã�b��4a+3��


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ1������OAB����OCD�У�OA=OB��OC=OD����AOB=��COD=40��������AC��BD���ڵ�M����գ�
��![]() ��ֵΪ�� ����
��ֵΪ�� ����
�ڡ�AMB�Ķ���Ϊ�� ����
��2�����̽��
��ͼ2������OAB����OCD�У���AOB=��COD=90�㣬��OAB=��OCD=30��������AC��BD���ӳ����ڵ�M�����ж�![]() ��ֵ����AMB�Ķ�������˵�����ɣ�
��ֵ����AMB�Ķ�������˵�����ɣ�
��3����չ����
�ڣ�2���������£�����OCD�Ƶ�O��ƽ������ת��AC��BD����ֱ�߽��ڵ�M����OD=1��OB=![]() ����ֱ��д������C���M�غ�ʱAC�ij���
����ֱ��д������C���M�غ�ʱAC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����![]() Ԫ�ļ۸�һ��������������ۣ���۾ָ����г�����涨�����۵��۲�����
Ԫ�ļ۸�һ��������������ۣ���۾ָ����г�����涨�����۵��۲�����![]() Ԫ�Ҳ�����
Ԫ�Ҳ�����![]() Ԫ���������з��֣��ÿ������ÿ����������
Ԫ���������з��֣��ÿ������ÿ����������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����ij�ֺ�����ϵ����Ӧ���£�
��Ԫ��֮�����ij�ֺ�����ϵ����Ӧ���£�
���۵��� |
|
|
|
|
|
�������� |
|
|
|
|
|
��1��������ѧ���ĺ���֪ʶ�����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�����ʸÿ�����ÿ������![]() ��Ԫ�������ֵ�Ƕ��٣�
��Ԫ�������ֵ�Ƕ��٣�
��3������ÿ�����ÿ��������벻����![]() Ԫ�������ÿ����������
Ԫ�������ÿ����������![]() ����Ϊ���ٱ���
����Ϊ���ٱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ20cm����ABC��120��������P��Qͬʱ�ӵ�A����������P��4cm/s���ٶȣ���A��B��C��·�����C�˶���Q����2![]() cm/s���ٶ���A��O��·�����O�˶���Ȼ������2cm/s���ٶ���O��D��·�����D�˶�����P��Q�����յ�ʱ�������˶���֮���������˶�ʱ��Ϊt�룮
cm/s���ٶ���A��O��·�����O�˶���Ȼ������2cm/s���ٶ���O��D��·�����D�˶�����P��Q�����յ�ʱ�������˶���֮���������˶�ʱ��Ϊt�룮
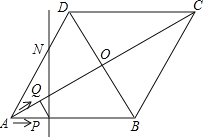
��1���ڵ�P��AB���˶�ʱ���ж�PQ��Խ���AC��λ�ù�ϵ����˵�����ɣ�
��2������Q��������ABCD�ĶԽ��߽���O�ĶԳƵ�ΪM������P�Ҵ�ֱ��AB��ֱ��l������ABCD�ı�AD����CD���ڵ�N��
��ֱ��д������PQM��ֱ��������ʱt��ȡֵ��Χ��
���Ƿ����������t��ʹ��PMN����PNΪһֱ�DZߵ�ֱ�������Σ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
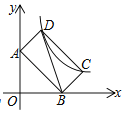
����Ŀ����ͼ������ABCD�ı�AB�Ľ���ʽΪy��ax+2������C��D��˫����y��![]() ��k��0���ϣ���AB��2AD����k��_____��
��k��0���ϣ���AB��2AD����k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������������ҩ����.�������Ĺ����У��Ⱦ���![]() ��ҩ�O���������ٷ������
��ҩ�O���������ٷ������![]() ��Ȼ���ٴ�������ͨ��.��֪����ÿ���������к�ҩ��
��Ȼ���ٴ�������ͨ��.��֪����ÿ���������к�ҩ��![]() ��
��![]() ����ҩ���ڿ����еij���ʱ��
����ҩ���ڿ����еij���ʱ��![]() ��
��![]() ��֮��ĺ���ͼ����ͼ��ʾ�������ڴ���ͨ��ǰ
��֮��ĺ���ͼ����ͼ��ʾ�������ڴ���ͨ��ǰ![]() ��
��![]() �ֱ���������һ�κ�������ͨ���
�ֱ���������һ�κ�������ͨ���![]() ��
��![]() ���㷴��������.
���㷴��������.
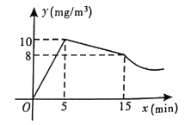
��1�����������Ĺ�ϵʽ��
��2���������ڿ����к�ҩ��������![]() �ҳ���ʱ�䲻����
�ҳ���ʱ�䲻����![]() ��������Чɱ���������ʴ˴������Ƿ���Ч��
��������Чɱ���������ʴ˴������Ƿ���Ч��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���εο쳵��һ�ֱ�ݵij��й��ߣ�ij�صļƼ۹��������
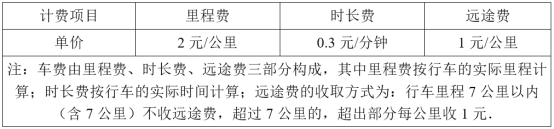
С����С�ŷֱ�Ӳ�ͬ�ص㣬����ͬʱ�����εο쳵����ͬһ�ص��������֪����Լ���ص�ʱ���ǵ�ʵ���г���̷ֱ�Ϊ7������9������˸����εο쳵�ij˳�����ͬ������һ���ȵ���Լ���ص㣬���Ⱥ���һ�˵�ʱ��������Լ�ʵ�ʳ˳�ʱ�䣬��ǡ������һ��ʵ�ʳ˳�ʱ���һ�룬��С��ij˳���Ϊ_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ŀ��ȵ���Ϊ10Ԫ/����Ϊ�������˿ͣ��õ깲�Ƴ������ֻ�Ա�������±���
��Ա������ | �쿨����/Ԫ | ��Ч�� | �Żݷ�ʽ |
A�� | 40 | 1�� | ÿ������� |
B�� | 80 | 1�� | ÿ������� |
C�� | 130 | 1�� | һ���Թ���2�����ڶ������ |
���磬����A���Ա����1���ڹ���50�ο��ȣ�ÿ�ι���2����������![]() Ԫ����С��1�����ڸñ����깺�ȵĴ�������75~85��֮�䣬��ÿ�ι���2��������ʡǮ�ķ�ʽΪ�� ��
Ԫ����С��1�����ڸñ����깺�ȵĴ�������75~85��֮�䣬��ÿ�ι���2��������ʡǮ�ķ�ʽΪ�� ��
A.����A���Ա��B.����B���Ա��
C.����C���Ա��D.�������Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ�����ͼ����㣨4����5���ͣ�0��3��������x�ύ�ڵ�M����1��0����N��
��1����˶��κ����Ľ���ʽ��
��2���������κ�����ͼ��Ķ���Ϊ��P����O������ԭ�㣬����OPN�������
��3�������R���P����x��Գƣ��ж���M��N��P��RΪ������ı��εı�֮���λ���������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com