
【题目】如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
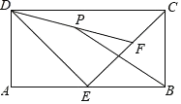
A.2B.4C.![]() D.2
D.2![]()
【答案】D
【解析】
根据中位线定理可得出点点P的运动轨迹是经过CD中点并且平行于EC的一条线段,再根据垂线段最短可得当BP⊥P1P2时,PB取得最小值;由矩形的性质以及已知的数据即可知BP1⊥P1P2,故BP的最小值为BP1的长,由勾股定理求解即可.
解:如图: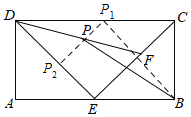
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2= ![]() CE
CE
当点F在EC上除点C、E的位置处时,有DP=FP
由中位线定理可知:P1P∥CE且P1P= ![]() CF
CF
∴点P的运动轨迹是线段P1P2,
∴当BP⊥P1P2时,PB取得最小值
∵矩形ABCD中,AB=4,AD=2,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=2
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°
∴∠DP2P1=90°
∴∠DP1P2=45°
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长
在等腰直角BCP1中,CP1=BC=2
![]()
∴PB的最小值是![]()
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了丰富学生课余生活,计划开设以下课外活动项目:A—版画,B—机器人,C—航模,D—园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
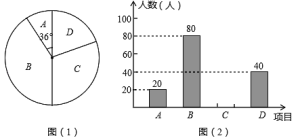
(1)这次被调查的学生共有 人;扇形统计图中,选“D—园艺种植”的学生人数所占圆心角的度数是 °
(2)请你将条形统计图补充完整;
(3)若该校学生总数为1000人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
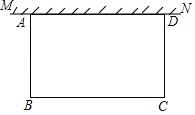
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠ABC=90°,AB=BC=4,点O是边AC的中点,连接OB,将△AOB绕点A顺时针旋转α°至△ANM,连接CM,点P是线段CM的中点,连接PB,PN.

(1)如图1,当α=180时,请直接写出线段PN和PB之间满足的位置和数量关系;
(2)如图2,当0<α<180时,请探索线段PN和PB之间满足何位置和数量关系?证明你的结论
(3)当△AOB旋转至C,M,N三点共线时,线段BP的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=240cm,AB=120cm,球目前在G点位置,AG=80cm,如果小丁瞄准BC边上的点F将球打过去,经过点F反弹后碰到CD边上的点H,再经过点H反弹后,球刚好弹到AD边的中点E处落袋.

(1)求证:△BGF∽△DHE;
(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
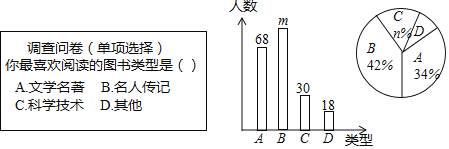
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,点A(3,3),点B(4,0),点C(0,-1).
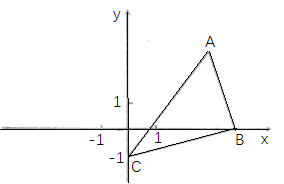
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,
①点A经过的路径AA’的长为________;(结果保留![]() )
)
②写出B’的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
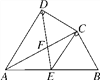
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com