
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
两点,且 ![]() ;下列等边三角形
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
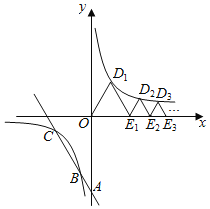
【答案】![]() ; 60
; 60
【解析】
设![]() ,设直线与
,设直线与![]() 轴的交点为H,先求解
轴的交点为H,先求解![]() 的坐标,得到∠HAO=30°,用含
的坐标,得到∠HAO=30°,用含![]() 的代数式表示
的代数式表示![]() ,联立函数解析式利用根与系数的关系得到关于
,联立函数解析式利用根与系数的关系得到关于![]() 的方程,从而可得第一空的答案;过
的方程,从而可得第一空的答案;过![]() 分别向
分别向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]()
![]() 先根据等边三角形的性质与反比例函数的性质求解
先根据等边三角形的性质与反比例函数的性质求解![]() 的边长,依次同法可得后面等边三角形的边长,发现规律,再前25个等边三角形的周长之和即可.
的边长,依次同法可得后面等边三角形的边长,发现规律,再前25个等边三角形的周长之和即可.
解:设![]() ,设直线与
,设直线与![]() 轴的交点为H,
轴的交点为H,
令![]() 则
则![]()
![]()
令![]() 则
则![]()
∴H(![]() ),又A(0,b),
),又A(0,b),
![]()
∴tan∠HAO=![]() ,∴∠HAO=30°,
,∴∠HAO=30°,
过![]() 作
作![]() 轴于
轴于![]()
![]() 作
作![]() 轴于
轴于![]() ,
,
∴AB=2BM,AC=2CN,∵BM=![]() ,
,![]() ,
,
∴AB=![]() ,AC=
,AC=![]() ,
,
∴![]() ,
,
联立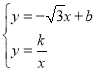
得到![]() 。
。
∴![]() ,由已知可得
,由已知可得![]() ,
,
∴![]() ,
,
∴反比例函数的解析式为![]() ,
,
过![]() 分别向
分别向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]()
![]()
设
由等边三角形的性质得:![]()
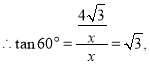
得:![]()
![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
可得![]() 的边长为4,
的边长为4,
同理设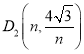 ,
,
![]()
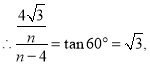
![]()
解得:![]() (舍去)
(舍去)
经检验:![]() 符合题意,
符合题意,
![]()
![]()
![]() 的边长为
的边长为![]() ,
,
同理可得:![]()
![]() 的边长为
的边长为![]() ,
,
![]()
![]() 的边长为
的边长为![]() .
.
∴前25个等边三角形的周长之和为![]()
=![]()
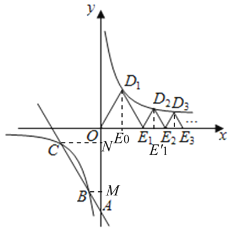
故答案为:![]()


科目:初中数学 来源: 题型:
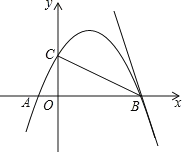
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 交二次函数
交二次函数![]() 的图像于点
的图像于点![]() ,
,![]() ,点
,点![]() 在该二次函数的图像上,设过点
在该二次函数的图像上,设过点![]() (其中
(其中![]() )且平行于
)且平行于![]() 轴的直线交直线
轴的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,以线段
,以线段![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .
.

(1)若点![]() 的横坐标为8.
的横坐标为8.
①用含![]() 的代数式表示
的代数式表示![]() 的坐标;
的坐标;
②点![]() 能否落在该二次函数的图像上?若能,求出
能否落在该二次函数的图像上?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(2)当![]() 时,若点
时,若点![]() 恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线
恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
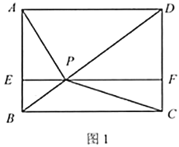
【题目】(1)如图1,点![]() 为矩形
为矩形![]() 对角线
对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .若
.若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
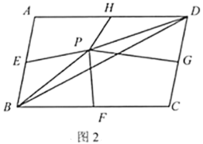
(2)如图2,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上),点
上),点![]() 、
、![]() 、
、![]() 、
、![]() 分别为各边的中点.设四边形
分别为各边的中点.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
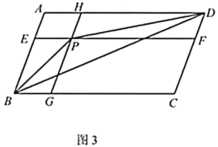
(3)如图3,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上)过点
上)过点![]() 作
作![]() ,
,![]() ,与各边分别相交于点
,与各边分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() .设四边形
.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
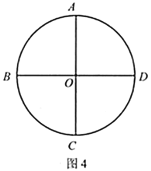
(4)如图4,点![]() 、
、![]() 、
、![]() 、
、![]() 把
把![]() 四等分.请你在圆内选一点
四等分.请你在圆内选一点![]() (点
(点![]() 不在
不在![]() 、
、![]() 上),设
上),设![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .根据你选的点
.根据你选的点![]() 的位置,直接写出一个含有
的位置,直接写出一个含有![]() 、
、![]() 、
、![]() 、
、![]() 的等式(写出一种情况即可).
的等式(写出一种情况即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,双曲线![]() 与直线
与直线![]() 相交于点
相交于点![]() 和B,过B点作
和B,过B点作![]() 轴于点C,连接AC,已知
轴于点C,连接AC,已知![]() .
.
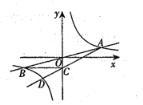
(1)求![]() 的值;
的值;
(2)延长AC交双曲线于另一点D,求D的的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 抛物线的顶点,对称轴与
抛物线的顶点,对称轴与![]() 轴交于点
轴交于点![]() .
.
⑴.求抛物线的解析式;
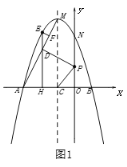
⑵.如图1,连接![]() ,点
,点![]() 是线段
是线段![]() 上方抛物线上的一动点,
上方抛物线上的一动点,![]() 于点
于点![]() ;过点
;过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 取最大值时.
取最大值时.
①.求![]() 的最小值;
的最小值;
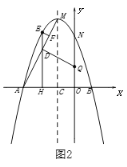
②.如图2,![]() 点是
点是![]() 轴上一动点,请直接写出
轴上一动点,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
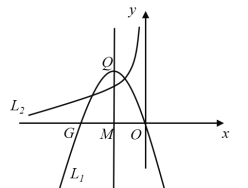
【题目】如图,抛物线L1:![]() (常数t>0)与
(常数t>0)与![]() 轴的负半轴交于点G,顶点为Q,过Q作QM⊥
轴的负半轴交于点G,顶点为Q,过Q作QM⊥![]() 轴交
轴交![]() 轴于点M,交双曲线L2:
轴于点M,交双曲线L2:![]()
![]() 于点P,且OG·MP=4.
于点P,且OG·MP=4.
(1)求![]() 值;
值;
(2)当t=2时,求PQ的长;
(3)当P是QM的中点时,求t的值;
(4)抛物线L1与抛物线L2所围成的区域(不含标界)内整点(点的横、纵坐标都是整数)的个数有且只有1个,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字![]() 、1、2,它们除了数字不同外,其它都完全相同.
、1、2,它们除了数字不同外,其它都完全相同.
(1)随机地从布袋中摸出一个小球,求摸出的球为标有数字1的小球的概率.
(2)小红先从布袋中随机摸出一个小球,记下数字作为![]() 的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为
的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为![]() 的值,请用树状图或表格列出
的值,请用树状图或表格列出![]() 、
、![]() 的所有可能的值,并求出直线
的所有可能的值,并求出直线![]() 不经过第四象限的概率.
不经过第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就会产生余数,现在我们利用整数的除法运算来研究一种数——“差一数”.
定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为“差一数”.
例如:![]() ,
,![]() ,所以14是“差一数”;
,所以14是“差一数”;
![]() ,但
,但![]() ,所以19不是“差一数”.
,所以19不是“差一数”.
(1)判断49和74是否为“差一数”?请说明理由;
(2)求大于300且小于400的所有“差一数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com