
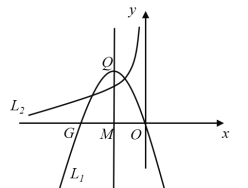
【题目】如图,抛物线L1:![]() (常数t>0)与
(常数t>0)与![]() 轴的负半轴交于点G,顶点为Q,过Q作QM⊥
轴的负半轴交于点G,顶点为Q,过Q作QM⊥![]() 轴交
轴交![]() 轴于点M,交双曲线L2:
轴于点M,交双曲线L2:![]()
![]() 于点P,且OG·MP=4.
于点P,且OG·MP=4.
(1)求![]() 值;
值;
(2)当t=2时,求PQ的长;
(3)当P是QM的中点时,求t的值;
(4)抛物线L1与抛物线L2所围成的区域(不含标界)内整点(点的横、纵坐标都是整数)的个数有且只有1个,直接写出t的取值范围.
【答案】(1)k=-2;(2)PQ=![]() ;(3)t=4;(4)
;(3)t=4;(4)![]() .
.
【解析】
(1)由题意得G点和M点的坐标,可得OG=t,根据OG·MP=4,可得MP![]() ,可得出P的坐标,把P代入
,可得出P的坐标,把P代入![]() ,即可得出答案;
,即可得出答案;
(2)先根据题意得出Q的坐标为(-1,![]() ),P的横坐标为-1,把x=-1代入
),P的横坐标为-1,把x=-1代入![]() 求出y,即可求出答案;
求出y,即可求出答案;
(3)根据题意表示出Q的坐标和P的坐标,把P代入![]() 即可得出答案;
即可得出答案;
(4)根据题意得由L1与L2围成的区域只有一个整点,分①当x=-2时,![]() 满足1<y≤2和当x=-3时,
满足1<y≤2和当x=-3时,![]() 满足1<y≤2;②当x=-2时,
满足1<y≤2;②当x=-2时,![]() 满足2<y≤3和当x=-3时,
满足2<y≤3和当x=-3时,![]() 满足0≤y≤1,两种情况讨论即可.
满足0≤y≤1,两种情况讨论即可.
(1)由题意得G的坐标为(-t,0),
∴M点的坐标为(![]() ,0),
,0),
∴OG=t,
∵OG·MP=4,
∴MP=![]() ,
,
∴P的坐标为(![]() ,
,![]() ),
),
把P(![]() ,
,![]() )代入
)代入![]() ,得
,得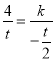 ,
,
解得k=-2;
(2)由(1)得双曲线L2:![]() ,
,
当t=2时,抛物线L1:![]() ,
,
∴Q的坐标为(-1,![]() ),P的横坐标为-1,
),P的横坐标为-1,
当x=-1时,在![]() 中,y=
中,y=![]() =2,
=2,
∴PQ=2-![]() =
=![]() ;
;
(3)抛物线L1: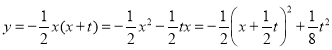 ,
,
∴Q的坐标为(![]() ,
,![]() ),
),
∵P是QM的中点,
∴P的坐标为(![]() ,
,![]() ),
),
把P(![]() ,
,![]() )代入
)代入![]() 得:
得: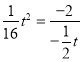 ,
,
解得:t=4;
(4)由L1与L2围成的区域只有一个整点,
①如图,L1具有对称性,
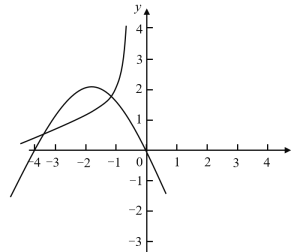
∴当x=-2时,![]() 满足1<y≤2,
满足1<y≤2,
∴1<t-2≤2,
解得3<t≤4,
当x=-3时,![]() 满足1<y≤2,
满足1<y≤2,
∴1<![]() (t-3)≤2,
(t-3)≤2,
![]() <t-3≤
<t-3≤![]() ,
,
![]() ,
,
∴t的取值范围是![]() ;
;
②如图:
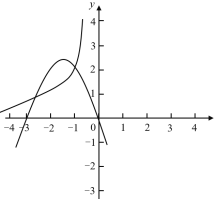
当x=-2时,![]() 满足2<y≤3,
满足2<y≤3,
∴2<t-2≤3,
解得4<t≤5,
当x=-3时,![]() 满足0≤y≤1,
满足0≤y≤1,
∴0≤![]() (t-3)≤1,
(t-3)≤1,
0≤t-3≤![]() ,
,
![]() ,
,
此时无解;
综上:t的取值范围是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
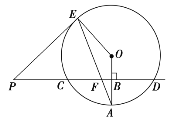
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)若PF=13,求PE的长;
(3)在(2)的条件下,sinA=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2021年起,江苏省高考采用“![]() ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是________;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2中选化学、生物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
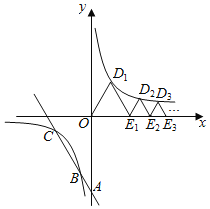
【题目】如图, 直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与双曲线
,与双曲线![]() 在第三象限交于
在第三象限交于![]() 两点,且
两点,且 ![]() ;下列等边三角形
;下列等边三角形![]() ,
,![]() ,
,![]() ,……的边
,……的边![]() ,
,![]() ,
,![]() ,……在
,……在![]() 轴上,顶点
轴上,顶点![]() ……在该双曲线第一象限的分支上,则
……在该双曲线第一象限的分支上,则![]() = ____,前25个等边三角形的周长之和为 _______.
= ____,前25个等边三角形的周长之和为 _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | a |
12000≤x<16000 | b | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | 2 | 0.04 |
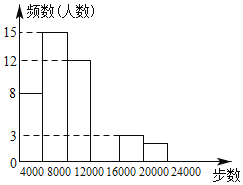
请根据以上信息,解答下列问题:
(1)写出a,b的值并补全频数分布直方图;
(2)我市约有5000名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
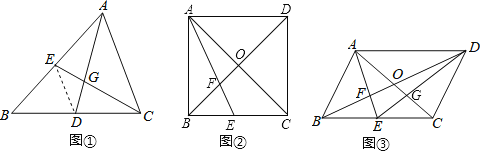
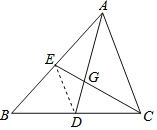
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .垂直于
.垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,记
,记![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.5<s<6B.6<s<7C.7<s<8D.8<s<9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com