【题目】如图，在平面直角坐标系中，双曲线
与直线
相交于点
和B，过B点作
轴于点C，连接AC，已知
．
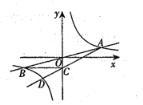
（1）求
的值；
（2）延长AC交双曲线于另一点D，求D的的坐标．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过点
，
，直线
交
轴于点
，且与抛物线交于
、
两点．
为抛物线上一动点（不与点，重合）．
（1）求抛物线的解析式；
（2）当点在直线
上方时，过点作
轴交于点
，
轴交于点
，求
的最大值；
（3）设
为直线上的点，以，
，，为顶点的四边形能否构成平行四边形？若能，请直接写出点的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有4张正面分别写有数字1、2、3、4的卡片，将4张卡片的背面朝上，洗匀．
（1）若从中任意抽取1张，抽的卡片上的数字恰好为3的概率是________；
（2）若先从中任意抽取1张（不放回），再从余下的3张中任意抽取1张，求抽得的2张卡片上的数字之和为3的倍数的概率．（请用“画树状图”或“列表”等方法写出分析过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从2021年起，江苏省高考采用“
”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选科，“2”是指在化学、生物、思想政治、地理4科中任选2科．
（1）若小丽在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是________；
（2）若小明在“1”中选择了物理，用画树状图的方法求他在“2中选化学、生物的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
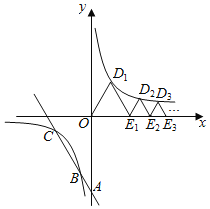
【题目】如图， 直线
与
轴交于点
，与双曲线
在第三象限交于
两点，且 
；下列等边三角形
，
，
，……的边
，
，
，……在
轴上，顶点
……在该双曲线第一象限的分支上，则
= ____，前25个等边三角形的周长之和为 _______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l1：y=﹣
x与反比例函数y=
的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2：
（1）求反比例函数的表达式；
（2）将直线l1：y=﹣x向上平移后的直线l2与反比例函数y=在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
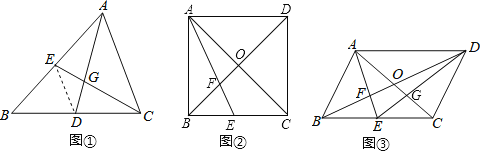
【题目】教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．
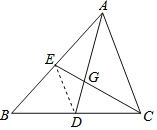
例2 如图，在
中，
分别是边
的中点，
相交于点
，求证：
，
证明：连结
．
请根据教材提示，结合图①，写出完整的证明过程．
结论应用：在
中，对角线
交于点
，
为边
的中点，
、
交于点
．
（1）如图②，若为正方形，且
，则
的长为 ．
（2）如图③，连结
交
于点，若四边形
的面积为
，则的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
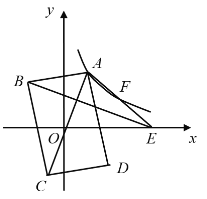
【题目】如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE．若AD平分
，反比例函数
的图象经过AE上的两点A，F，且
，
的面积为18，则k的值为（ ）
A.6B.12C.18D.24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
